题目内容

3．已知关于x的方程x2+ax+2b-2=0（a，b∈R）有两个相异实根，若其中一根在区间（0，1）内，另一根在区间（1，2）内，则$\frac{b-4}{a-1}$的取值范围是$（{\frac{1}{2}，\frac{3}{2}}）$．

分析 由题意知$\left\{\begin{array}{l}{2b-2＞0}\\{1+a+2b-2＜0}\\{4+2a+2b-2＞0}\end{array}\right.$，从而转化为线性规划问题求解即可．

解答 解：令f（x）=x2+ax+2b-2，
由题意知，
$\left\{\begin{array}{l}{2b-2＞0}\\{1+a+2b-2＜0}\\{4+2a+2b-2＞0}\end{array}\right.$，
作其表示的平面区域如下，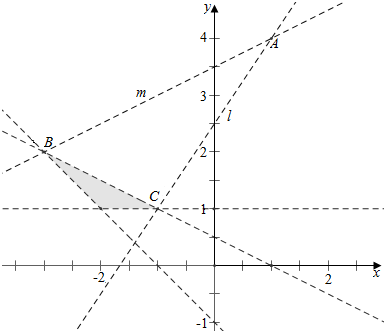
，
$\frac{b-4}{a-1}$的几何意义是点A（1，4）与阴影内的点的连线的斜率，
直线m过点B（-3，2），故km=$\frac{2-4}{-3-1}$=$\frac{1}{2}$；
直线l过点C（-1，1），故kl=$\frac{1-4}{-1-1}$=$\frac{3}{2}$；
结合图象可知，
$\frac{b-4}{a-1}$的取值范围是$（{\frac{1}{2}，\frac{3}{2}}）$；
故答案为：$（{\frac{1}{2}，\frac{3}{2}}）$．

点评 本题考查了二次函数与二次方程的关系应用及线性规划的变形应用．

练习册系列答案
相关题目
13．已知函数f（x）=sin（x-α）+2cosx，（其中α为常数），给出下列五个命题：
①存在α，使函数f（x）为偶函数；
②存在α，使函数f（x）为奇函数；
③函数f（x）的最小值为-3；
④若函数f（x）的最大值为h（α），则h（α）的最大值为3；
⑤当α=$\frac{π}{6}$时，（-$\frac{π}{3}$，0）是函数f（x）的一个对称中心．
其中正确的命题序号为①④⑤（把所有正确命题的选号都填上）
14．已知实数a∈[0，10]，那么方程x2-ax+9=0有实数解的概率是$\frac{2}{5}$．
11．已知函数f（x）=$\frac{{e}^{x}}{a}$-$\frac{a}{{e}^{x}}$（a＞0）是定义在R上的奇函数．
（1）求a的值；
（2）设函数g（x）=1-$\frac{2a}{{2}^{x}+1}$，判断g（x）的单调性，并用定义证明你的结论；
（3）当x∈[0，ln4]，求函数h（x）=e2x+meax的最小值．
18．判断下列函数是否有极值，如果有极值，请求出其极值；若无极值，请说明理由．
（1）y=8x3-12x2+6x+1；
（2）y=$\frac{2x}{{x}^{2}+1}$-2．
8．若函数f（x）=ax3+bx2+cx在x=±1处有极值，且f（-1）=-1，求a，b，c．
15．设数列{an}的前n项和为Sn，已知a1=1，Sn=$\frac{{（{n+1}）}}{2}{a_n}$，n∈N*．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）若数列{bn}满足：对任意的正整数n，都有a1b1+a2b2+…+anbn=（n-1）•2n+1，求数列$\left\{{\frac{S_n}{b_n}}\right\}$的最大项．
12．已知函数f（x）=2acos2ωx+2sinωxcosωx．（ω＞0）
（1）若f（x）的最大值为$\sqrt{2}-1$，求实数a的值．
（2）在条件（1）下，把f（x）图象上的点的横坐标变为原来的3倍，纵坐标不变，可得函数y=$\sqrt{2}$sin（$\frac{2}{3}$x-$\frac{π}{4}$）-1的图象，求ω的值；
（3）若$ω=\frac{1}{2}$，图象关于直线x=$\frac{5}{3}$π对称，求函数y=cosx+asinx的对称轴．
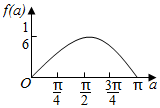
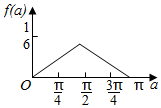
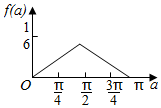
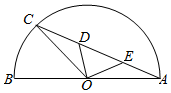13．如图，$\widehat{AB}$为半圆，O为圆心，OA=1，C为$\widehat{AB}$上的动点，D、E为线段AC的三等分点，设∠AOC=α，将△ODE的面积为y=f（α），则y=f（α）的图象大致为（　　）
A．B．
C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网