题目内容
已知定义在区间[-π,
(1)求函数y=f(x)在[-π,![]() π]的表达式;
π]的表达式;
(2)求方程f(x)=![]() 的解.
的解.
解析:(1)当x∈[-![]() ,
,![]() π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-![]() <φ<
<φ<![]() ),
),
观察图象易得:A=1,ω=1,φ=![]() ,
,
即x∈[-![]() ,
,![]() π]时,
π]时,
函数f(x)=sin(x+![]() ).
).
由函数y=f(x)的图象关于直线x=-![]() 对称得,x∈[-π,-
对称得,x∈[-π,-![]() ]时,函数f(x)=-sinx.
]时,函数f(x)=-sinx.
∴f(x)=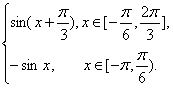
(2)当x∈[-![]() ,
,![]() ]时,由sin(x+
]时,由sin(x+![]() )=
)=![]() 得,x+
得,x+![]() =
=![]() 或
或![]()
![]() x=-
x=-![]() 或x=
或x=![]() ;
;
当x∈[-π,-![]() ]时,由 -sinx=
]时,由 -sinx=![]() 得,x=-
得,x=-![]() 或x=-
或x=-![]() .
.
∴方程f(x)=![]() 的解集为{-
的解集为{-![]() ,-
,-![]() ,-
,-![]() ,
,![]() }.
}.

练习册系列答案
相关题目
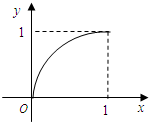 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: