题目内容

已知定义在区间[-π，
3π
2
]上的函数y=f（x）图象关于直线x=
π
4
对称，当x≥
π
4
时，f（x）=-sinx．
（1）作出y=f（x）的图象；
（2）求y=f（x）的解析式．
分析：（1）根据条件可得函数y=f（x）的图象．
（2）任取x∈[-π，
π
4
]，则
π
2
-x∈[
π
4
，
3π
2
]，由f（x）=f（
π
2
-x）可得f（x）的解析式，即可得到y=f（x）的解析式
解答：解：（1）根据条件可得函数y=f（x）的图象如图所示：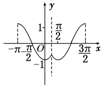
（2）任取x∈[-π，
π
4
]，则
π
2
-x∈[
π
4
，
3π
2
]，
因函数y=f（x）图象关于直线x=
π
4
对称，则f（x）=f（
π
2
-x）．
又当x≥
π
4
时，f（x）=-sinx，则f（x）=f（
π
2
-x）=-sin（
π
2
-x）=-cosx，
可得函数的解析式为 f（x）=
-cosx，x∈[-π，
π
4
]
-sinx，x∈[
π
4
，
3π
2
]
．
点评：本题主要考查三角函数的图象和性质，求函数的解析式，属于中档题．
练习册系列答案
相关题目
已知定义在区间（-1，1）上的函数f(x)=
ax+b
x2+1
为奇函数．且f(
1
2
)=
2
5
．
（1）、求实数a、b的值．
（2）、求证：函数f（x）在区间（-1，1）上是增函数．
（3）、解关于t的不等式f（t-1）+f（t）＜0．
已知定义在区间（0，+∞）上的函数f（x）满足f（
x1x2
）=f（x1）-f（x2），且当x＞1时，f（x）＜0．
（1）求f（1）的值；
（2）判断并证明f（x）的单调性；
（3）若f（3）=-1，求f（x）在[2，9]上的最小值．
填空题
（1）已知
cos2x
sin(x+
π
4
)
=
4
3
，则sin2x的值为
1
9
1
9
．
（2）已知定义在区间[0，
3π
2
]上的函数y=f（x）的图象关于直线x=
3π
4
对称，当x≥
3π
4
时，f（x）=cosx，如果关于x的方程f（x）=a有四个不同的解，则实数a的取值范围为
(-1，-
2
2
)
(-1，-
2
2
)
．

（3）设向量
a
，
b
，
c
满足
a
+
b
+
c
=
0
，(
a
-
b
)⊥
c
，
a
⊥
b
，若|
a
|=1，则|
a
|2+|
b
|2+|
c
|2的值是
4
4
．
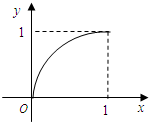精英家教网已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：
①f（x2）-f（x1）＞x2-x1；
②[f（x2）-f（x1）]•（x2-x1）＜0；
③x2f（x1）＞x1f（x2）；
④
f(x1)+f(x2)
2
＜f(
x1+x2
2
)．
其中正确的结论的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网