题目内容
(本小题满分12分)
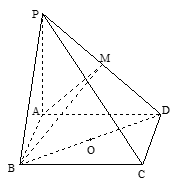
四棱锥 ,面
,面 ⊥面
⊥面 .侧面
.侧面 是以
是以 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 为直角梯形,
为直角梯形, ,
,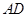 ∥
∥ ,
, ⊥
⊥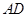 ,
, 为
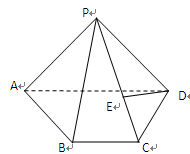
为 上一点,且
上一点,且 .
.
(Ⅰ)求证 ⊥
⊥ ;
;
(Ⅱ)求二面角 的正弦值.
的正弦值.
(Ⅰ)先证 ⊥面
⊥面 ,再证
,再证 ⊥面
⊥面 ,进而得证;
,进而得证;
(Ⅱ)
解析试题分析:(Ⅰ)面 ⊥面
⊥面 且交线为
且交线为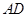 又
又 ⊥
⊥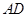 ,
,
∴ ⊥面
⊥面 ,
,
∴ ⊥
⊥ , ……3分
, ……3分
∵ ⊥
⊥ ,
, ,
,
∴ ⊥面
⊥面 ,
,
 , ……5分
, ……5分
∴ ⊥
⊥ . ……6分
. ……6分
(Ⅱ)设 为
为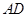 中点,则
中点,则 ⊥
⊥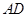 ,∴
,∴ ⊥面
⊥面 ,
,
建系如图,则



 ,
,
∴ ,
, , ……8分
, ……8分
设 为面
为面 的法向量,
的法向量,
则 ,∴
,∴ 为面
为面 的一个法向量, ……9分
的一个法向量, ……9分 为面
为面 的法向量, ……10分
的法向量, ……10分
∴ , ……11分
, ……11分
∴二面角 的正弦值为
的正弦值为 . ……12分
. ……12分
考点:本小题主要满足空间中线线垂直的证明和二面角的求解.
点评:用定理证明立体几何问题时要紧扣定理,定理中要求的条件一个也不能漏;用空间向量求解二面角时,要仔细计算,还要注意题目中的二面角时锐角还是钝角.

练习册系列答案
相关题目
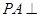 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙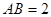 ,
, 是⊙
是⊙ ,
,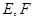 分别为
分别为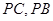 中点。
中点。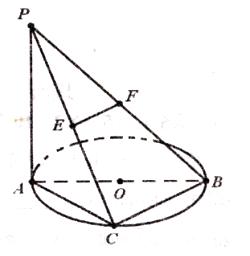
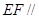 平面
平面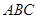 ;
;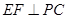 ;
;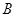 -
-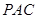 的体积。
的体积。
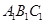 中,
中,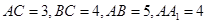 ,点
,点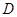 是
是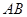 的中点.
的中点. 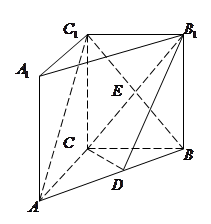
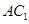 ∥平面
∥平面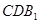 ;
;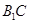 所成的角的余弦值;
所成的角的余弦值;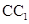 与平面
与平面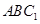 所成角的正弦值;
所成角的正弦值; 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱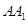 ⊥BD,点F为
⊥BD,点F为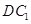 的中点.
的中点.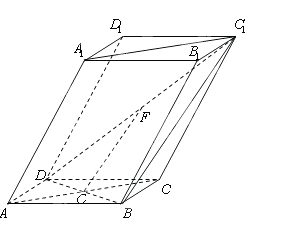
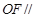 平面
平面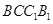 ;
;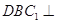 平面
平面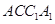 .
. 
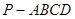 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面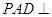 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.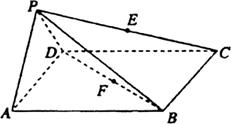
 平面PAD;
平面PAD; 平面PAD;
平面PAD; 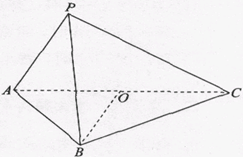
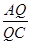 的值;若不存在,说明理由。
的值;若不存在,说明理由。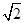 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
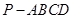 中,底面
中,底面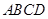 是矩形,
是矩形,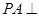 平面
平面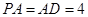 ,
,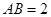 .以
.以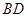 的中点
的中点 为球心、
为球心、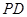 于点
于点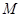 .
.
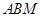 ;
; 与平面
与平面