题目内容
(本小题满分16分)
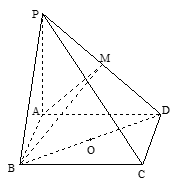
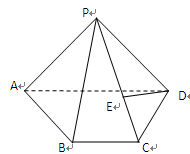
如图,在四棱锥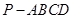 中,底面
中,底面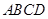 是矩形,
是矩形,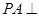 平面
平面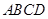 ,
,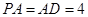 ,
,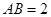 .以
.以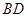 的中点
的中点 为球心、
为球心、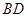 为直径的球面切
为直径的球面切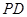 于点
于点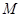 .
.
(1)求证:PD⊥平面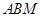 ;
;
(2)求直线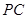 与平面
与平面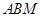 所成的角的正弦值;
所成的角的正弦值;
(3)求点 到平面
到平面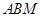 的距离.
的距离.
(1)先证 ,推出
,推出 ,证明
,证明 ;
;
(2) ;(3)
;(3)
解析试题分析:(1)证:依题设, 在以
在以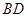 为直径的球面上,则
为直径的球面上,则 ,……2分
,……2分
因为 ,则
,则 ,又
,又 ,
,
所以 ,则
,则 , ……4分
, ……4分
因此有 , ……5分
, ……5分
(2)如图所示,建立空间直角坐标系,则 ,
, ,
, ,
,  ,
, ,
, , ……8分
, ……8分
设平面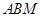 的一个法向量
的一个法向量 ,由
,由 可得:
可得: ,
,
令 ,则
,则 ,即
,即 . ……10分
. ……10分
设所求角为 ,则
,则 , ……12分
, ……12分
(3)设所求距离为 ,由
,由 ,得:
,得: ……16分
……16分
考点:本题主要考查立体几何中线面平行、垂直、角和距离的计算,空间向量的应用
点评:典型题,立体几何中平行、垂直关系的证明及角的计算问题是高考中的必考题,通过建立适当的坐标系,应用空间向量,可使问题简化。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,面
,面 ⊥面
⊥面 .侧面
.侧面 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 ,
,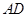 ∥
∥ ,
, ⊥
⊥ 为
为 上一点,且
上一点,且 .
.
 ⊥
⊥ ;
; 的正弦值.
的正弦值. ,
, ,
,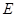 是
是 的中点,
的中点, 是
是 中点.
中点.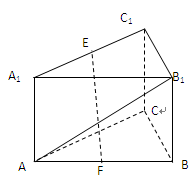
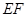 ∥面
∥面 ;
;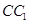 所成角的正切值;
所成角的正切值;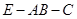 的平面角为
的平面角为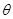 ,求
,求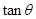 的值.
的值. 中,
中,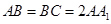
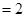 ,
, ,
, 是
是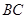 的中点.
的中点.
 平行平面
平行平面 ;
; 的余弦值;
的余弦值;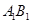 上是否存在点
上是否存在点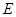 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定 ,已知在四棱锥
,已知在四棱锥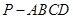 中,底面
中,底面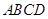 是矩形,
是矩形,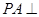 平面
平面 ,
, ,
,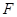 是
是 的中点,
的中点,  是线段
是线段 上的点.
上的点.
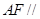 平面
平面 ;
; 的大小为
的大小为 ,试确定
,试确定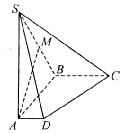
 ,求sin
,求sin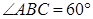 ,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.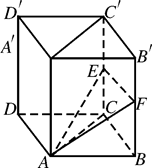
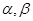 ,
,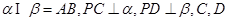 是垂足.
是垂足.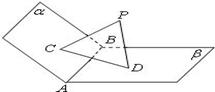
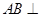 平面
平面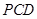 ;
; 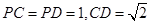 ,求证:
,求证: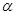
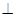
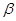 .
.