题目内容
13．cos20°+cos60°+cos100°+cos140°的为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 运用诱导公式化为cos100°=-cos80°，cos140°=-cos40°，再由80°=60°+20°，40°=60°-20°，运用两角和差的余弦公式，即可得到所求值．
解答 解：cos20°+cos60°+cos100°+cos140°
=cos20°+$\frac{1}{2}$-cos80°-cos40°
=cos20°+$\frac{1}{2}$-cos（60°+20°）-cos（60°-20°）
=cos20°+$\frac{1}{2}$-（$\frac{1}{2}$cos20°-$\frac{\sqrt{3}}{2}$sin20°）-（$\frac{1}{2}$cos20°+$\frac{\sqrt{3}}{2}$sin20°）
=cos20°+$\frac{1}{2}$-cos20°=$\frac{1}{2}$．
故选：B．
点评 本题考查诱导公式和两角和差的余弦公式，注意角的变换，考查运算能力，属于中档题．
练习册系列答案
相关题目
18．已知圆C：（x-1）2+（y-2）2=25，直线l：my-x+3-m=0，当直线l被圆C截得的弦最短时的m的值是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | -$\frac{1}{2}$ | D． | -2 |
5．
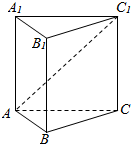如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，直线AC1与平面BCC1B1所成角的余弦值等于（ ）
如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，直线AC1与平面BCC1B1所成角的余弦值等于（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{10}}{5}$ | C． | $\frac{\sqrt{5}}{4}$ | D． | $\frac{\sqrt{10}}{4}$ |