题目内容
已知椭圆 :
: .
.
(1) 椭圆 的短轴端点分别为
的短轴端点分别为 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆 交于
交于 两点,其中点
两点,其中点 满足
满足 ,且
,且 .
.
①证明直线 与
与 轴交点的位置与
轴交点的位置与 无关;
无关;
②若∆ 面积是∆
面积是∆ 面积的5倍,求
面积的5倍,求 的值;
的值;
(2)若圆 :
: .
. 是过点
是过点 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中 交圆
交圆 于
于 、
、 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .求
.求 面积取最大值时直线
面积取最大值时直线 的方程.
的方程.

解:(1)①因为 ,M (m,
,M (m, ),且
),且 ,
,
 直线AM的斜率为k1=
直线AM的斜率为k1= ,直线BM斜率为k2=
,直线BM斜率为k2= ,
,
 直线AM的方程为y=
直线AM的方程为y= ,直线BM的方程为y=
,直线BM的方程为y= ,
,
 由
由 得
得 ,
,


由 得
得 ,
,

 ;
;
据已知, ,
,
 直线EF的斜率
直线EF的斜率

 直线EF的方程为
直线EF的方程为  ,
,
令x=0,得
 EF与y轴交点的位置与m无关.
EF与y轴交点的位置与m无关.
② ,
, ,
, ,
,
 ,
,
 ,
,
 ,
,



 ,
,
 整理方程得
整理方程得 ,即
,即 ,
,
又有 ,
,
 ,
,  ,
, 为所求.
为所求.
(2) 因为直线 ,且都过点
,且都过点 ,所以设直线
,所以设直线 ,
,
直线 , …
, …
所以圆心 到直线
到直线 的距离为
的距离为 ,
,
所以直线 被圆
被圆 所截的弦
所截的弦 ;
;
由 ,所以
,所以
 所以
所以 
所以 
当 时等号成立,
时等号成立,
此时直线

练习册系列答案
相关题目
 ,集合∁UA={y|y=x
,集合∁UA={y|y=x ,
, 吨,每次都购买
吨,每次都购买 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为 万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.
万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨. 的三内角
的三内角 、
、 、
、 所对边的边长分别为
所对边的边长分别为 、
、 、
、 ,且
,且  ,
, , 则
, 则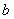 的取值范围为………( ).
的取值范围为………( ).
 .
. 
 .
.
 .
. 
 .
. 是方程
是方程 的两根,则
的两根,则 =_______.
=_______. 表示选出的志愿者中女生的人数,则随机变量
表示选出的志愿者中女生的人数,则随机变量 =_____(结果用最简分数表示).
=_____(结果用最简分数表示).  的左焦点
的左焦点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,双曲线左顶点为
,双曲线左顶点为 ,若
,若 ,则该双曲线的离心率为
,则该双曲线的离心率为 B.
B.  C.
C. D.
D. 
 是
是 的一个内角,且
的一个内角,且 ,则
,则 表示( )
表示( ) 轴上的椭圆 B.焦点在
轴上的椭圆 B.焦点在 轴上的椭圆
轴上的椭圆