题目内容
底面半径为1的圆柱形容器里放有四个半径为0.5的实心铁球,四个球两两相切,其中底层两球与容器底面相切,现往容器里注水,使水面恰好浸没所有铁球,则容器中水高为 .(提示:正方体中构造正四面体)
考点:球内接多面体
专题:计算题,球
分析:先确定四个球心构成的四面体的形状,在底面的射影,构成一个正方形,边长为正四面体的对棱的距离,从而求出注水高.
解答:
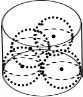 解:设四个实心铁球的球心为O1,O2,O3,O4,其中O1,O2为下层两球的球心,
解:设四个实心铁球的球心为O1,O2,O3,O4,其中O1,O2为下层两球的球心,
则O1O2O3O4是一个棱长为1的正四面体.A,B,C,D分别为四个球心在底面的射影,ABCD是一个边长为
的正方形,正方形的边长就是正四面体对棱的距离:
.
注水高为小球的直径与正四面体对棱距离的和.
所以注水高为1+
.
故答案为:1+
.
 解:设四个实心铁球的球心为O1,O2,O3,O4,其中O1,O2为下层两球的球心,
解:设四个实心铁球的球心为O1,O2,O3,O4,其中O1,O2为下层两球的球心,则O1O2O3O4是一个棱长为1的正四面体.A,B,C,D分别为四个球心在底面的射影,ABCD是一个边长为
| ||
| 2 |
| ||
| 2 |
注水高为小球的直径与正四面体对棱距离的和.
所以注水高为1+
| ||
| 2 |
故答案为:1+
| ||
| 2 |
点评:本题考查球的内接多面体知识,考查空间想象能力以及学生分析解决问题的能力,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知点P(x,y)的坐标x,y满足
,则x2+y2-4x的取值范围是( )
|
| A、[0,12] |
| B、[-1,12] |
| C、[3,16] |
| D、[-1,16] |
已知a=log20.5,b=0.2-0.1,c=0.21.1,则a,b,c的大小关系是( )
| A、a<b<c |
| B、c<a<b |
| C、a<c<b |
| D、b<c<a |
某几何体的三视图如图所示,则此几何体的体积是( )


A、
| ||
| B、6π | ||
C、
| ||
D、
|
 如图,设D是边长为l的正方形区域,E是D内函数y=
如图,设D是边长为l的正方形区域,E是D内函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
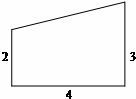 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是 如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)
如图,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积,(其中∠BAC=30°)