题目内容
15.函数y=$\frac{1}{\sqrt{3}-tanx}$的定义域为(-$\frac{π}{2}$+kπ,$\frac{π}{3}$+kπ)∪($\frac{π}{3}$+kπ,$\frac{π}{2}$+kπ),k∈Z.分析 根据函数y的解析式,分母不为0,结合正切函数的定义域,即可写出函数y的定义域.
解答 解:∵函数y=$\frac{1}{\sqrt{3}-tanx}$,
∴$\sqrt{3}$-tanx≠0,
即tanx≠$\sqrt{3}$;
解得x≠$\frac{π}{3}$+kπ,且k∈Z,
∴函数y的定义域为(-$\frac{π}{2}$+kπ,$\frac{π}{3}$+kπ)∪($\frac{π}{3}$+kπ,$\frac{π}{2}$+kπ),k∈Z.
故答案为:(-$\frac{π}{2}$+kπ,$\frac{π}{3}$+kπ)∪($\frac{π}{3}$+kπ,$\frac{π}{2}$+kπ),k∈Z.
点评 本题考查了正切函数的图象与性质的应用问题,也考查了求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
20.已知sin2θ=$\frac{3}{5}$,且0<2θ<$\frac{π}{2}$,则$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$的值为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
3.已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:关于x的函数y=(2a-1)x在[1,+∞)上是减函数.若“p且q”为真命题,则实数a的取值范围是( )
| A. | (-∞,$\frac{2}{3}$] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$] | D. | ($\frac{1}{2}$,1) |
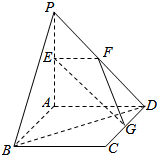 平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点
平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点