题目内容
15.函数f(x)=sinx(x∈[0,2π])的单调递减区间是[$\frac{π}{2}$,$\frac{3π}{2}$].分析 根据正弦函数的图象可得答案.
解答 解:函数f(x)=sinx(x∈[0,2π])
其图象为:
从图象可是单调递减区间为[$\frac{π}{2}$,$\frac{3π}{2}$]
故答案为:[$\frac{π}{2}$,$\frac{3π}{2}$]
点评 本题考查了正弦函数的图象及性质.属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
10.已知函数f(x)=(x2-2mx+m2)lnx无极值点,则实数m的取值范围是( )
| A. | (-∞,$-2{e}^{-\frac{3}{2}}$) | B. | (-∞,1] | C. | (-2,0)∪(0,1] | D. | (-∞,$-2{e}^{-\frac{3}{2}}$]∪{1} |
7.袋中装有大小相同的四个球,四个球上分别标有数字“2”,“3”,“4”,“6”,现从中随机选取三个球,则所选的三个球上的数字能构成等差数列的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
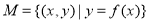 ,若对于任意
,若对于任意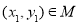 ,存在
,存在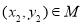 ,使得
,使得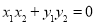 成立,则称集合
成立,则称集合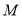 是“理想集合”.给出下列5个集合:
是“理想集合”.给出下列5个集合: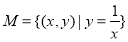 ;
;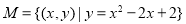 ;
; ;
;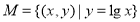 ;
; .
. ,
, ,则
,则 的值为 .
的值为 .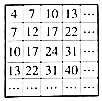 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.