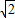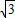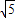题目内容
已知各顶点都在球面上的正四棱锥的高为3,体积为6,则这个球的表面积是
- A.8π
- B.16π
- C.

- D.

B
分析:正四棱锥P-ABCD的五个顶点在同一球面上,则其外接球的球心在它的高PO1上,记为O,如图.求出AO1,OO1,解出球的半径,求出球的表面积;
解答:正四棱锥的高为3,体积为6,易知底面面积为6,边长为 .
.
正四棱锥P-ABCD的外接球的球心在它的高PO1上,
记为O,PO=AO=R,PO1=3,OO1=3-R,
在Rt△AO1O中,AO1= AC=
AC= ,由勾股定理R2=3+(3-R)2得R=2,
,由勾股定理R2=3+(3-R)2得R=2,
∴球的表面积S=16π
故选B
点评:本题考查球的表面积,球的内接体问题,解答关键是确定出球心的位置,利用直角三角形列方程式求解球的半径.需具有良好空间形象能力、计算能力.
分析:正四棱锥P-ABCD的五个顶点在同一球面上,则其外接球的球心在它的高PO1上,记为O,如图.求出AO1,OO1,解出球的半径,求出球的表面积;
解答:正四棱锥的高为3,体积为6,易知底面面积为6,边长为
 .
.正四棱锥P-ABCD的外接球的球心在它的高PO1上,

记为O,PO=AO=R,PO1=3,OO1=3-R,
在Rt△AO1O中,AO1=
 AC=
AC= ,由勾股定理R2=3+(3-R)2得R=2,
,由勾股定理R2=3+(3-R)2得R=2,∴球的表面积S=16π
故选B
点评:本题考查球的表面积,球的内接体问题,解答关键是确定出球心的位置,利用直角三角形列方程式求解球的半径.需具有良好空间形象能力、计算能力.

练习册系列答案
相关题目
 ,则这个直三棱柱的体积等于
,则这个直三棱柱的体积等于

 ,若球O的体积为
,若球O的体积为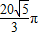 ,则这个直三棱柱的体积等于( )
,则这个直三棱柱的体积等于( )