题目内容
已知直三棱柱ABC-A1B1C1的各顶点都在球O的球面上,且AB=AC=1,BC=
,若球O的体积为
π,则这个直三棱柱的体积等于( )
| 3 |
20
| ||
| 3 |
分析:根据直三棱柱的性质和球的对称性,得球心O是△ABC和△A1B1C1的外心连线段的中点,连接OA、OB、OC、O1A、O1B、O1C.在△ABC中利用正、余弦定理算出O1A=1,由球O的体积算出OA=
,然后在Rt△O1OA中,用勾股定理算出O1O=2,得三棱柱的高O1O2=4,最后算出底面积S△ABC=
,可得此直三棱柱的体积.
| 5 |
| ||
| 4 |
解答:解: 设△ABC和△A1B1C1的外心分别为O1、O2,连接O1O2,
设△ABC和△A1B1C1的外心分别为O1、O2,连接O1O2,
可得外接球的球心O为O1O2的中点,连接OA、OB、OC、O1A、O1B、O1C
△ABC中,cosA=
=-
∵A∈(0,π),∴A=
根据正弦定理,得△ABC外接圆半径O1A=
=1
∵球O的体积为V=
=
π,∴OA=R=
Rt△O1OA中,O1O=
=2,可得O1O2=2O1O=4
∵直三棱柱ABC-A1B1C1的底面积S△ABC=
AB•ACsin
=
∴直三棱柱ABC-A1B1C1的体积为S△ABC×O1O2=
故选:B
 设△ABC和△A1B1C1的外心分别为O1、O2,连接O1O2,
设△ABC和△A1B1C1的外心分别为O1、O2,连接O1O2,可得外接球的球心O为O1O2的中点,连接OA、OB、OC、O1A、O1B、O1C
△ABC中,cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
| 1 |
| 2 |
∵A∈(0,π),∴A=
| 2π |
| 3 |
根据正弦定理,得△ABC外接圆半径O1A=
| BC |
| 2sinA |
∵球O的体积为V=
| 4πR3 |
| 3 |
20
| ||
| 3 |
| 5 |
Rt△O1OA中,O1O=
| OA2-O1A 2 |
∵直三棱柱ABC-A1B1C1的底面积S△ABC=
| 1 |
| 2 |
| 2π |
| 3 |
| ||
| 4 |
∴直三棱柱ABC-A1B1C1的体积为S△ABC×O1O2=
| 3 |
故选:B
点评:本题给出直三棱柱的底面三角形的形状和外接球的体积,求此三棱柱的体积,着重考查了球的体积公式式、直三棱柱的性质和球的对称性等知识,属于中档题.

练习册系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.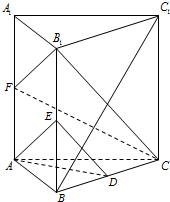 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.