Question

18.设F₁、F₂为椭圆=1的两个焦点，P为椭圆上的一点，已知P、F₁、F₂是一个直角三角形的三

 

个顶点，且|PF₁|>|PF₂|，求的值.

Answer 1

18.［解法一］由已知|PF₁|+|PF₂|=6，|F₁F₂|=2.                  

根据直角的不同位置，分两种情况：

若∠PF₂F₁为直角，则|PF₁|²=|PF₂|²+|F₁F₂|²，

即|PF₁|²=(6－|PF₁|)²+20，

 

得|PF₁|=，|PF₂|=，故；        

 

若∠F₁PF₂为直角，则|F₁F₂|²=|PF₁|²+|PF₂|²，

 

即20=|PF₁|²+(6－|PF₁|)²，

 

得|PF₁|=4，|PF₂|=2，故.            

 

［解法二］由椭圆的对称性不妨设P(x，y)(x>0，y>0)，

则由已知可得F₁(－，0)，F₂(，0).    

根据直角的不同位置，分两种情况：

若∠PF₂F₁为直角，则P(，)，

 

于是|PF₁|=，|PF₂|=，故；    

 

若∠F₁PF₂为直角，则.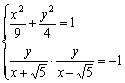

 

解得x=，y=，即P(，)，

 

于是|PF₁|=4，|PF₂|=2，故.