题目内容
在平面直角坐标系中,已知矩形ABCD,AB=2,BC=1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合.将矩形折叠,使A点落在线段DC上.若折痕所在直线的斜率为k,试写出折痕所在直线的方程.
解 (1)当k=0时,此时A点与D点重合,折痕所在的直线方程为y= .
.
(2)当k≠0时,将矩形折叠后A点落在线段CD上的点为G(a,1).所以A与G关于折痕所在的直线对称,
有kAG·k=-1, k=-1⇒a=-k.
k=-1⇒a=-k.
故G点坐标为G(-k,1),从而折痕所在的直线与AG的交点坐标(线段AG的中点)为M .
.
折痕所在的直线方程为y- =k
=k ,
,
即y=kx+ +
+ .
.
∴k=0时,y= ;k≠0时,y=kx+
;k≠0时,y=kx+ +
+ .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
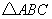 中,
中,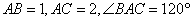 ,点
,点 是边
是边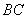 上的动点,动点
上的动点,动点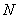 满足
满足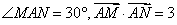 (点
(点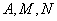 按逆时针方向排列).
按逆时针方向排列).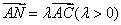 ,求
,求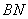 的长;
的长;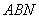 面积的最大值.
面积的最大值.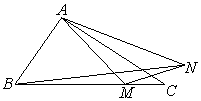
 上的两点A、B满足
上的两点A、B满足 ,则弦AB的中点到准线的距离为 。
,则弦AB的中点到准线的距离为 。 时,直线l1:kx-y=k-1与直线l2:ky-x=2k的交点在( ).
时,直线l1:kx-y=k-1与直线l2:ky-x=2k的交点在( ).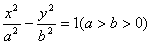 ,以右焦点F为圆心,|OF|为半径的圆交双曲线两渐近线于点M、N (异于原点O),若|MN|=
,以右焦点F为圆心,|OF|为半径的圆交双曲线两渐近线于点M、N (异于原点O),若|MN|=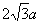 ,则双曲线C的离心率 是 ( )
,则双曲线C的离心率 是 ( )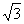 C.
C. 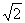 D.
D.