题目内容
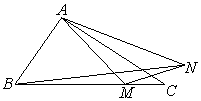
如图,已知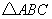 中,
中,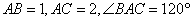 ,点
,点 是边
是边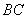 上的动点,动点
上的动点,动点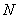 满足
满足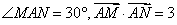 (点
(点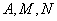 按逆时针方向排列).
按逆时针方向排列).
(1)若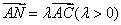 ,求
,求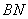 的长;
的长;
(2)求△ 面积的最大值.
面积的最大值.
 |
解:(1)由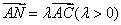 得点
得点 在射线
在射线 上,
上, ,
,
因为 的面积等于△
的面积等于△ 与△
与△ 面积的和,
面积的和,
所以 ,
,
得: ,
,
又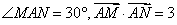 ,所以
,所以 ,即
,即 ,
,
 ,即
,即 ;
;
(2)设 ,则
,则 ,因为
,因为 的面积等于△
的面积等于△ 与△
与△ 面积的和,所以
面积的和,所以 ,
,
得: ,
,
又 ,所以
,所以 ,即
,即 ,
,
所以△ 的面积
的面积

即
(其中: 为锐角),
为锐角),
所以当 时,△
时,△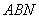 的面积最大,最大值是
的面积最大,最大值是 .
.

练习册系列答案
相关题目
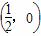 ,直线l:x=-
,直线l:x=-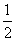 ,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l. ,面积为
,面积为 ,则扇形的圆心角的弧度数是
,则扇形的圆心角的弧度数是 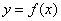 对任意的
对任意的 满足
满足 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是
的导函数),则下列不等式成立的是 B.
B. C.
C. D.
D.
 ,若类似上面各式方法将
,若类似上面各式方法将 分拆得到的等式右边最后一个数是
分拆得到的等式右边最后一个数是 ,则正整数
,则正整数 等于____.
等于____. 禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ).
禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ). B. C. D.
B. C. D.  是坐标原点,点
是坐标原点,点 ,若点
,若点 为平面区域
为平面区域 上的一个动点,则
上的一个动点,则 的取值范围是( ).
的取值范围是( ).  B.
B. C.
C. D.
D.
 的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率等于 ( )
相切,则该双曲线的离心率等于 ( ) B.
B. C.
C. D.
D.