题目内容
如图，空间四边形ABCD中，E，F，G，H分别是直线AB，BC，CD，DA上的点，如果EF∩GH=Q，则点Q在直线上．
- A.BD
- B.AB
- C.AC
- D.CD
C
分析：利用线面位置关系即可知道分别在两个相交平面的两相交直线的交点必在两平面的交线上．
解答：如图所示：
∵EF?平面ABC，GH?平面ACD，平面ABC∩平面ACD=AC，
∴EF∩GH=Q必在直线AC上．
故选C．
点评：正确理解线面位置关系是解题的关键．
分析：利用线面位置关系即可知道分别在两个相交平面的两相交直线的交点必在两平面的交线上．
解答：如图所示：
∵EF?平面ABC，GH?平面ACD，平面ABC∩平面ACD=AC，
∴EF∩GH=Q必在直线AC上．
故选C．
点评：正确理解线面位置关系是解题的关键．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
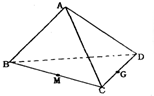如图，空间四边形ABCD中，M、G分别是BC、CD的中点，则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，空间四边形ABCD的对棱AD、BC成60°的角，且AD=BC=4，平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H．
如图，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且
如图，空间四边形ABCD中，E、F分别是AB、AD的中点，G、H分别在BC、CD上，且BG：GC=DH：HC=1：2