题目内容
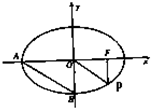
如图,F是椭圆![]() (a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为
(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为![]() .点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:
.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:![]() 相切.
相切.
![]() (Ⅰ)求椭圆的方程:
(Ⅰ)求椭圆的方程:
![]()
 (Ⅱ)过点A的直线l2与圆M交于PQ两点,且
(Ⅱ)过点A的直线l2与圆M交于PQ两点,且![]() ,求直线l2的方程.
,求直线l2的方程.
解析:(1)F(-c,0),B(0,![]() ),∵kBF=
),∵kBF=![]() ,kBC=-
,kBC=-![]() ,C(3c,0)
,C(3c,0)
![]() 且圆M的方程为(x-c)2+y2=4c2,圆M与直线l1:x+
且圆M的方程为(x-c)2+y2=4c2,圆M与直线l1:x+![]() y+3=0相切,
y+3=0相切,
![]() ∴
∴  ,解得c=1,
,解得c=1,
![]() ∴所求的椭圆方程为
∴所求的椭圆方程为![]() 6分
6分
![]() (2) 点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,
(2) 点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,
![]() 过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2),
过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2),
∵![]() ,又
,又![]() ,∴cos<
,∴cos<![]() >=
>=
∴∠PMQ=120°,圆心M到直线l2的距离d=![]() ,所以
,所以 ,∴k=
,∴k=![]()
所求直线的方程为x±2![]() +2=0. 14分
+2=0. 14分

练习册系列答案
相关题目
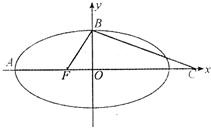 如图,F是椭圆
如图,F是椭圆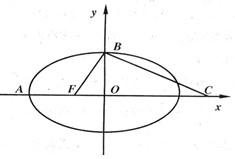 如图,F是椭圆
如图,F是椭圆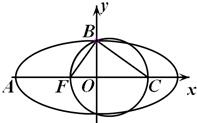 如图,F是椭圆
如图,F是椭圆