题目内容
1.用三角函数线比较sinl与cosl的大小,结果是sinl>cosl.分析 画出图形运用三角函数数线的定义,直角三角形结合大小判断即可.
解答 解:∵$\frac{π}{4}$$<1<\frac{π}{3}$,
∴Rt△OAM中,OM<AM
根据三角函数线的定义得出:OM=cosl,AM=sinl,
∴sinl>cosl.
故答案为:sinl>cosl.
点评 本题考查了三角函数的定义,数形结合的思想,关键画出图,运用直角三角形判断即可.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
6.在△ABC中,角A,B满足sin$\frac{3A}{2}$=sin$\frac{3B}{2}$,则三边a,b,c必满足( )
| A. | a=b | B. | a=b=c | ||
| C. | a+b=2c | D. | (a-b)(a2+b2-ab-c2)=0 |
10.若α∈(π,2π),则$\sqrt{\frac{1+cosα}{2}}$化简的结果为( )
| A. | sin$\frac{α}{2}$ | B. | cos$\frac{α}{2}$ | C. | -sin$\frac{α}{2}$ | D. | -cos$\frac{α}{2}$ |
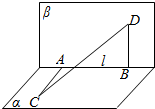 已知A,B是直二面角α-l-β的棱上两点,线段AC⊆α,线段BD⊆β,且AC⊥l,BD⊥l,AC=AB=6,BD=24,求线段CD的长.
已知A,B是直二面角α-l-β的棱上两点,线段AC⊆α,线段BD⊆β,且AC⊥l,BD⊥l,AC=AB=6,BD=24,求线段CD的长.