题目内容
10.过A(0,0),B(6,0),C(0,4)三点的圆的方程(x-3)2+(y-2)2=13.分析 求出圆的圆心与半径,然后求解圆的方程.
解答 解:过A(0,0),B(6,0),C(0,4)三点的圆的圆心(3,2),半径为$\frac{1}{2}\sqrt{{4}^{2}+{6}^{2}}$=$\sqrt{13}$.
过A(0,0),B(6,0),C(0,4)三点的圆的方程:(x-3)2+(y-2)2=13.
故答案为:(x-3)2+(y-2)2=13.
点评 本题考查圆的方程的求法,求出圆的圆心与半径是解题的关键,考查计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
20.设等差数列{an}的前n项和为Sn,且a2+a7+a12=24,则S13=( )
| A. | 52 | B. | 78 | C. | 104 | D. | 208 |
1.不等式x2+x<$\frac{a}{b}$+$\frac{b}{a}$ 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-4)∪(2,+∞) |
18.化简$\sqrt{9{x^2}-6x+1}-{({\sqrt{3x-5}})^2}$,结果是( )
| A. | 6x-6 | B. | -6x+6 | C. | -4 | D. | 4 |
15.若已知sinθ-cosθ=$\frac{\sqrt{5}}{3}$,那么sin3θ-cos3θ的值为( )
| A. | $\frac{\sqrt{5}}{27}$ | B. | $\frac{11}{27}$ | C. | $\frac{11}{27}\sqrt{5}$ | D. | $\frac{25}{17}$ |
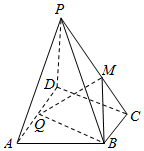 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.