题目内容
如图,已知在侧棱垂直于底面三棱柱 中,
中, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.
(1)求证: ;
;
(2)求证:
(3)求三棱锥 的体积.
的体积.
|
|
(1)证明:在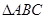 中,由勾股定理得
中,由勾股定理得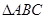 为直角三角形,即
为直角三角形,即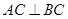 .又
.又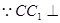 面
面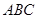 ,
,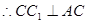 ,
,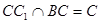 ,
,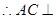 面
面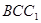 ,
,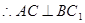 ;
;
(2)证明:设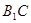 交
交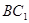 于点
于点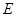 ,则
,则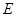 为
为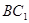 的中点,连接
的中点,连接 ,则
,则 为
为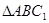 的中位线,
的中位线,
则在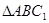 中,
中, ∥
∥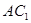 ,又
,又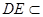 面
面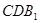 ,则
,则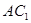 ∥面
∥面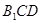 ;
;
(3)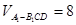 .
.
解析试题分析:(1)由勾股定理得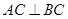 ,由
,由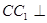 面
面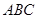 得到
得到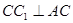 ,从而得到
,从而得到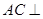 面
面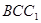 ,故
,故 ;(2)连接
;(2)连接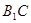 交
交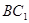 于点
于点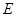 ,则
,则 为
为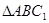 的中位线,得到
的中位线,得到 ∥
∥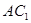 ,从而得到
,从而得到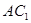 ∥面
∥面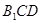 ;(3)过
;(3)过 作
作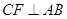 垂足为
垂足为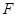 ,
,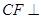 面
面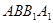 ,面积法求
,面积法求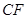 ,求出三角形
,求出三角形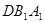 的面积,代入体积公式进行运算.
的面积,代入体积公式进行运算.
试题解析:(1)证明:在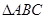 中,由勾股定理得
中,由勾股定理得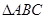 为直角三角形,即
为直角三角形,即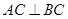 .
.
又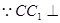 面
面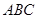 ,
,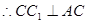 ,
,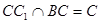 ,
,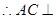 面
面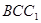 ,
,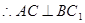 .
.
(2)证明:设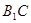 交
交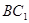 于点
于点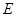 ,则
,则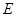 为
为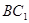 的中点,连接
的中点,连接 ,则
,则 为
为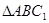 的中位线,
的中位线,
则在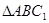 中,
中, ∥
∥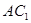 ,又
,又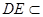 面
面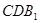 ,则
,则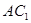 ∥面
∥面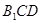 .
.
(3)在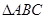 中过
中过 作
作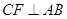 垂足为
垂足为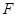 ,
,
由面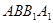 ⊥面
⊥面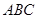 知,
知,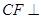 面
面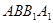 ,
,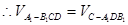 .
.
而 ,
,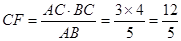 ,
,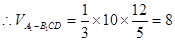 .
.
考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面 底面
底面 .
. 平面
平面 ;
; 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的余弦值.
的余弦值.
 中,
中, ⊥底面
⊥底面 ,底面
,底面 ,
, ,
, 分别是
分别是 ,
, 的 中点.
的 中点. 平面
平面 ;
; ;
; 是线段
是线段 上一动点,试确定
上一动点,试确定 平面
平面 ,并证明你的结论.
,并证明你的结论.

 中,已知平面
中,已知平面 平面
平面 且
且 ,
, .
.
 为棱
为棱 上的一点,且
上的一点,且 平面
平面 ,求线段
,求线段 的长度
的长度
 -A BC中,AB
-A BC中,AB  AC,AB=AC=2,
AC,AB=AC=2, =4,点D是BC的中点.
=4,点D是BC的中点. 与
与 所成角的余弦值;
所成角的余弦值; 与
与 所成二面角的正弦值.
所成二面角的正弦值.
 ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高) 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
, ,
, ,
, ,点
,点 、
、 、
、 分别为
分别为 、
、 、
、 的中点.
的中点. 平面
平面 ;
; 面
面 ;
; 的距离.
的距离.
 ,则AC与平面α所成角的大小是
,则AC与平面α所成角的大小是