题目内容
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(Ⅰ)如果P为线段VC的中点,求证:VA∥平面PBD;
(Ⅱ)如果正方形ABCD的边长为2,求三棱锥A-VBD的体积.
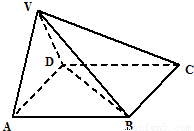
【答案】分析:(Ⅰ)连结AC与BD交于点O,连结OP,可得OP是△VAC的中位线,再根据线和平面平行的判定定理证得 VA∥平面PBD.
(Ⅱ)在平的面VAD内,过点V作VH⊥AD,则VH⊥面ABCD,再由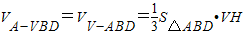 ,运算求得结果.
,运算求得结果.
解答: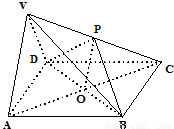 解:(Ⅰ)连结AC与BD交于点O,连结OP,
解:(Ⅰ)连结AC与BD交于点O,连结OP,
因为ABCD是正方形,所以OA=OC,又因为PV=PC
所以OP∥VA,又因为PO?面PBD,所以VA∥平面PBD.--------(6分)
(Ⅱ)在平的面VAD内,过点V作VH⊥AD,因为平面VAD⊥底面ABCD,所以VH⊥面ABCD.
所以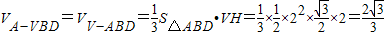 .------(12分)
.------(12分)
点评:本题主要考查直线和平面平行的判定定理的应用,用等体积法求棱锥的体积,属于中档题.
(Ⅱ)在平的面VAD内,过点V作VH⊥AD,则VH⊥面ABCD,再由
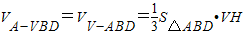 ,运算求得结果.
,运算求得结果.解答:
 解:(Ⅰ)连结AC与BD交于点O,连结OP,
解:(Ⅰ)连结AC与BD交于点O,连结OP,因为ABCD是正方形,所以OA=OC,又因为PV=PC
所以OP∥VA,又因为PO?面PBD,所以VA∥平面PBD.--------(6分)
(Ⅱ)在平的面VAD内,过点V作VH⊥AD,因为平面VAD⊥底面ABCD,所以VH⊥面ABCD.
所以
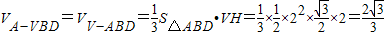 .------(12分)
.------(12分)点评:本题主要考查直线和平面平行的判定定理的应用,用等体积法求棱锥的体积,属于中档题.

练习册系列答案
相关题目
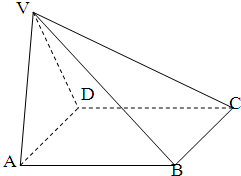 如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD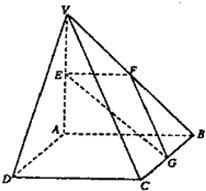 如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.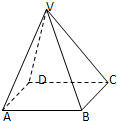 如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图:在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.