题目内容
【题目】设椭圆![]() :
:![]() (
(![]() ),左、右焦点分别是
),左、右焦点分别是![]() 、
、![]() 且
且![]() ,以
,以![]() 为圆心,3为半径的圆与以
为圆心,3为半径的圆与以![]() 为圆心,1为半径的圆相交于椭圆
为圆心,1为半径的圆相交于椭圆![]() 上的点
上的点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() :
:![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)运用圆与圆的位置关系,![]() 和
和![]() 的关系,计算即可得到
的关系,计算即可得到![]() ,进而得到椭圆
,进而得到椭圆![]() 的方程;
的方程;
(2)求得椭圆![]() 的方程,①设
的方程,①设![]() ,
,![]() ,求得
,求得![]() 的坐标,分别代入椭圆
的坐标,分别代入椭圆![]() 的方程,化简整理,即可得到所求值;
的方程,化简整理,即可得到所求值;
②设![]() ,
,![]() 将直线
将直线![]() 代入椭圆
代入椭圆![]() 的方程,运用韦达定理,三角形的面积公式,将直线
的方程,运用韦达定理,三角形的面积公式,将直线![]() 代入椭圆
代入椭圆![]() 的方程,由判别式大于0,可得
的方程,由判别式大于0,可得![]() 的范围,结合二次函数的最值,,
的范围,结合二次函数的最值,,![]() 的面积为
的面积为![]() ,即可得到所求的最大值.
,即可得到所求的最大值.
解:(1)由题意可知,![]() ,可得
,可得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]()
即有椭圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)知椭圆![]() 的方程为
的方程为![]() ,
,
①设![]() ,
,![]() ,由题意可知,
,由题意可知,
![]() ,由于
,由于![]() ,
,
代入化简可得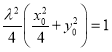 ,
,
所以![]() ,即
,即![]() ;
;
②设![]() ,
,![]() ,将直线
,将直线![]() 代入椭圆
代入椭圆![]() 的方程,可得
的方程,可得
![]()
![]() ,由
,由![]() ,可得
,可得![]() ,③
,③
则有![]() ,
,![]() ,
,
所以![]() ,
,
由直线![]() 与
与![]() 轴交于
轴交于![]() ,
,
则![]() 的面积为
的面积为![]()
![]()
设![]() ,则
,则![]() ,
,
将直线![]() 代入椭圆
代入椭圆![]() 的方程,
的方程,
可得![]()
![]() ,
,
由![]() 可得
可得![]() ,④
,④
由③④可得![]() ,则
,则![]() 在
在![]() 递增,即有
递增,即有![]() 取得最大值,
取得最大值,
即有![]() ,即
,即![]() ,取得最大值
,取得最大值![]() ,
,
由①知,![]() 的面积为
的面积为![]() ,
,
即![]() 面积的最大值为
面积的最大值为![]() .
.

 走进文言文系列答案
走进文言文系列答案【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
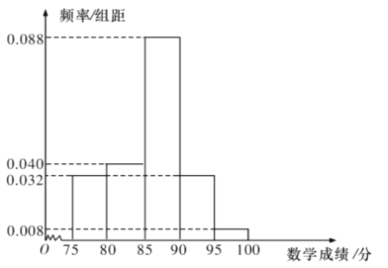
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②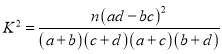 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |