题目内容
9.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?

分析 (Ⅰ)由已知作出频率分布表,由此能作出作出这些数据的频率分布直方图.
(II)由频率分布直方图能求出质量指标值的样本平均数、中位数位.
(Ⅲ)质量指标值不低于95的产品所占比例的估计值.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.
解答 解:(Ⅰ)由已知作出频率分布表为:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
| 频率 | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
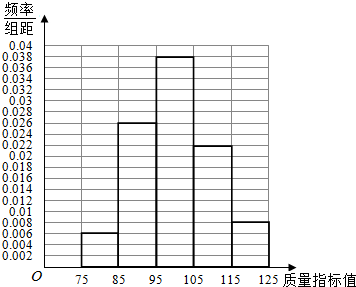
(II)质量指标值的样本平均数为:
$\overline{x}$=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
∵小矩形高度最高的位于区间[95,105),∴众数100.
∵[75,95)内频率为:0.06+0.26=0.32,
∴中位数位于[95,105)内,
设中位数为x,则x=95+$\frac{0.5-0.26-0.06}{0.38}×10$≈99.7,
∴中位数为99.7.…10 分
(Ⅲ)质量指标值不低于95 的产品所占比例的估计值为 0.38+0.22+0.08=0.68.
由于该估计值小于0.8,
故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.12 分
点评 本题考查频率分布直方图的作法,考查平均数、众数、中位数、方差的求法,考查产品质量指标所占比重的估计值的计算与应用,是基础题.

练习册系列答案
相关题目
14.已知角x的终边上一点坐标为$({sin\frac{5π}{6},cos\frac{5π}{6}})$,则角x的最小值为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{11π}{6}$ | D. | $\frac{2π}{3}$ |
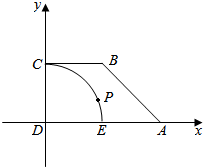 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.