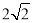题目内容
10.设集合A={x||x-a|<2},B={x|$\frac{1}{4}$<2x<8}.(1)若a=-1,求集合A;
(2)若A∩B=A,求实数a的取值范围.
分析 (1)把a的值代入A中不等式,求出解确定出A即可;
(2)求出B中不等式的解集确定出B,根据A与B的交集为A,得到A为B的子集,确定出a的范围即可.
解答 解:(1)把a=-1代入A中不等式得:|x+1|<2,
变形得:-2<x+1<2,
解得:-3<x<1,即A={x|-3<x<1};
(2)∵A∩B=A,A={x||x-a|<2}={x|a-2<x<a+2},B={x|$\frac{1}{4}$<2x<8}={x|-2<x<3},
∴A⊆B,
∴$\left\{\begin{array}{l}{a-2≥-2}\\{a+2≤3}\end{array}\right.$,
解得:0≤a≤1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
20.已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)+4f(-2)<0的解集为( )
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
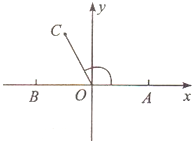 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.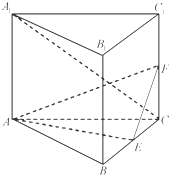 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.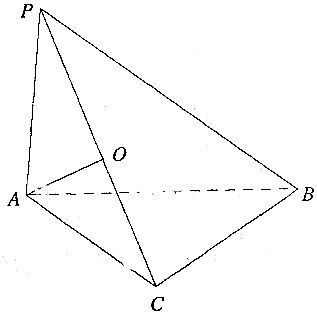 已知三棱锥P-ABC,PA⊥平面ABC,AC⊥BC,PA=2,AC=BC=1,则三棱锥P-ABC外接球的体积为$\sqrt{6}π$.
已知三棱锥P-ABC,PA⊥平面ABC,AC⊥BC,PA=2,AC=BC=1,则三棱锥P-ABC外接球的体积为$\sqrt{6}π$. ,函数
,函数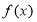 与
与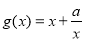 有相同极值点.
有相同极值点.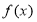 的最大值;
的最大值;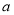 的值;
的值;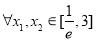 ,不等式
,不等式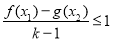 恒成立,求实数
恒成立,求实数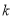 的取值范围.
的取值范围.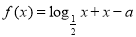 ,则“
,则“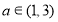 ”是“函数
”是“函数 在
在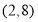 上存在零点”的( )
上存在零点”的( ) 表示的平面区域为
表示的平面区域为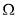 ,
,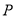 、
、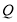 均为
均为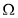 内一点,
内一点,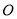 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )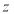 的最小值为
的最小值为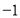 B.
B.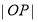 的最小值为
的最小值为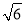
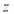 的最大值为
的最大值为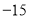 D.
D.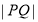 的最大值为
的最大值为