题目内容
（2013•丽水一模）若函数f（x）=
是奇函数，则a=
|
-1
-1
．分析：设x＜0，则-x＞0，由奇函数性质得f（-x）=-f（x）恒成立，代入表达式即可求得a值．
解答：解：设x＜0，则-x＞0，
由奇函数性质得f（-x）=-f（x）恒成立，即（-x）2-（-x）=-（ax2-x），
所以（a+1）x2=0恒成立，所以a=-1，
故答案为：-1．
由奇函数性质得f（-x）=-f（x）恒成立，即（-x）2-（-x）=-（ax2-x），
所以（a+1）x2=0恒成立，所以a=-1，
故答案为：-1．
点评：本题考查函数奇偶性的性质，属基础题，解决本题的关键是根据奇函数性质得到f（-x）=-f（x）恒等式．
练习册系列答案
相关题目
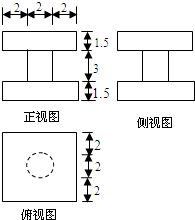（2013•丽水一模）某几何体的三视图如图所示，则该几何体的体积为
（2013•丽水一模）已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1），