题目内容
15.直三棱柱ABC-A1B1C1的三视图如图所示.
(1)求三棱柱ABC-A1B1C1的体积;
(2)若点D为棱AB的中点,求证:AC1∥平面CDB1.
分析 (1)由直三棱柱的三视图求出S△ABC,高BB1,由此能求出三棱柱ABC-A1B1C1的体积.
(2)连结B1C,BC1,交于点O,连结OD,则OD∥AC1,由此能证明AC1∥平面CDB1.
解答 解:(1)由直三棱柱的三视图得: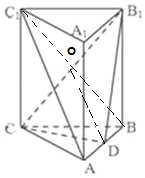
${S}_{ABC}=\frac{1}{2}×3×2=3$,高BB1=4,
∴三棱柱ABC-A1B1C1的体积V=S△ABC×BB1=3×4=12.
证明:(2)连结B1C,BC1,交于点O,连结OD,
∵点D为棱AB的中点,
∴OD∥AC1,
∵OD?平面CDB1,AC1?平面CDB1.
∴AC1∥平面CDB1.
点评 本题考查三棱锥的体积的求法,考查线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
11.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则弦AB的长为( )
| A. | 10 | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{13}{2}$ |
10.已知圆O的半径为2,PA、PB为圆O的两条切线,A、B为切点(A与B不重合),则$\overrightarrow{PA}$$•\overrightarrow{PB}$的最小值为( )
| A. | -12+4$\sqrt{2}$ | B. | -16+4$\sqrt{2}$ | C. | -12+8$\sqrt{2}$ | D. | -16+8$\sqrt{2}$ |
7.函数$f(x)=\frac{{3{x^2}}}{{\sqrt{1-x}}}+lg(3x+1)$的定义域是( )
| A. | $\left\{x|-\frac{1}{3}<x<1\right\}$ | B. | {x|x<1} | C. | $\left\{x|x>-\frac{1}{3}\right\}$ | D. | $\left\{x|x>1或x<-\frac{1}{3}\right\}$ |