题目内容
9.若a=33(10),b=52(6),c=11111(2),则三个数的大小关系是a>b>c.分析 分别将b,c转化为10进制,然后比较大小.
解答 解:将b,c都转化为10进制数,
b=52(6)=5×61+2=32,
c=11111(2)=1×24+1×23+1×22+1×2+1×20=31,
因为33>32>31,
所以a>b>c.
故答案为:a>b>c.
点评 本题考查的知识点是不同进制数之间的转换,解答的关键是熟练掌握不同进制之间数的转化规则,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.命题“若(a-2)(b-3)=0,则a=2或b=3”的否命题是( )
| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
14.复数$z=\frac{i^3}{i-1}$,则其共轭复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.在四面体S-ABCD中,$AB⊥BC,AB=BC=\sqrt{2}$SA=SC=SB=2,则该四面体外接球的表面积是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{10}{3}π$ | D. | $\frac{16}{3}π$ |
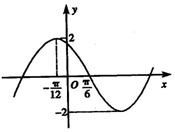 已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).
已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).