题目内容
9.已知△ABC的三顶点分别为A(1,4,1),B(1,2,3),C(2,3,1).则AB边上的高等于( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 利用向量共线的充要条件及向量垂直的充要条件列出方程组,求出$\overrightarrow{CD}$的坐标;利用向量模的坐标公式求出CD长.
解答 解:设$\overrightarrow{AD}$=λ$\overrightarrow{AB}$,又$\overrightarrow{AB}$=(0,-2,2).
则$\overrightarrow{AD}$=(0,-2λ,2λ).$\overrightarrow{AC}$=(1,-1,0),$\overrightarrow{CD}$=(-1,-2λ+1,2λ),
由$\overrightarrow{AB}$•$\overrightarrow{CD}$=0,
得λ=$\frac{1}{4}$,∴$\overrightarrow{CD}$=(-1,$\frac{1}{2}$,$\frac{1}{2}$),
∴|$\overrightarrow{CD}$|=$\frac{\sqrt{6}}{2}$.
故选:A.
点评 本题考查向量共线的充要条件、考查向量垂直的充要条件、考查向量模的坐标公式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4.已知m,n是两条不同直线,α,β是两个不同的平面,且n?β,则下列叙述正确的是( )
| A. | 若m∥n,m?α,则α∥β | B. | 若α∥β,m?α,则m∥n | C. | 若α∥β,m⊥n,则m⊥α | D. | 若m∥n,m⊥α,则α⊥β |
14.双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的虚轴长是( )
| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 8 |
19.将函数$y=3sin(2x+\frac{π}{6})$的图象上各点沿x轴向右平移$\frac{π}{6}$个单位长度,所得函数的解析式为( )
| A. | $y=3sin(2x-\frac{π}{6})$ | B. | y=3cos2x | C. | $y=3sin(2x+\frac{π}{3})$ | D. | y=3sin2x |
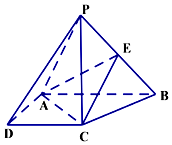 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.