题目内容
已知函数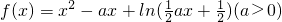 .
.
(1)当a=2时,求函数f(x)的单调区间;
(2)若对任意的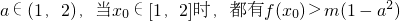 ,求实数m的取值范围.
,求实数m的取值范围.
解:(1)当a=2时,f(x)=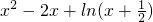 ,定义域为(-
,定义域为(- ,+∞).
,+∞).
f′(x)=2x-2+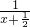 =2x-2+
=2x-2+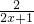 =
=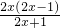 .
.
由f′(x)>0,得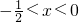 ,或x>
,或x> ;由f′(x)<0,得0<x<
;由f′(x)<0,得0<x< .
.
所以函数f(x)的单调递增区间为( ,0),(
,0),( ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0, ).
).
(2)y=f(x)的定义域为(- ,+∞).
,+∞).
f′(x)=2x-a+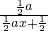 =2x-a+
=2x-a+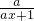 =
=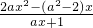 =
=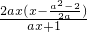 .
.
当1<a<2时,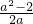 -1=
-1=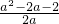 =
=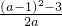 <0,即
<0,即 ,
,
所以当1<x<2时,f′(x)>0,f(x)在[1,2]上单调递增,
所以f(x)在[1,2]上的最小值为f(1)=1-a+ln(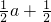 ).
).
依题意,对任意的a∈(1,2),当x0∈[1,2]时,都有f(x0)>m(1-a2),
即可转化为对任意的a∈(1,2),1-a+ln(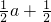 )-m(1-a2)>0恒成立.
)-m(1-a2)>0恒成立.
设g(a)=1-a+ln(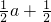 )-m(1-a2)(1<a<2).
)-m(1-a2)(1<a<2).
则g′(a)=-1+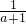 +2ma=
+2ma=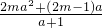 =
=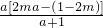 ,
,
①当m≤0时,2ma-(1-2m)<0,且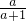 >0,所以g′(a)<0,
>0,所以g′(a)<0,
所以g(a)在(1,2)上单调递减,且g(1)=0,则g(a)<0,与g(a)>0矛盾.
②当m>0时,g′(a)=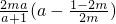 ,
,
若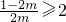 ,则g′(a)<0,g(a)在(1,2)上单调递减,且g(1)=0,g(a)<0,与g(a)>0矛盾;
,则g′(a)<0,g(a)在(1,2)上单调递减,且g(1)=0,g(a)<0,与g(a)>0矛盾;
若1<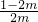 <2,则g(a)在(1,
<2,则g(a)在(1,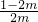 )上单调递减,在(
)上单调递减,在(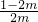 ,2)上单调递增,且g(1)=0,g(a)<g(1)=0,与g(a)>0矛盾;
,2)上单调递增,且g(1)=0,g(a)<g(1)=0,与g(a)>0矛盾;
若 ,则g(a)在(1,2)上单调递增,且g(1)=0,
,则g(a)在(1,2)上单调递增,且g(1)=0,
则恒有g(a)>g(1)=0,所以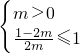 ,解得m
,解得m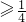 ,所以m的取值范围为[
,所以m的取值范围为[ ,+∞).
,+∞).
分析:(1)当a=2时,求出f(x),在定义域内解不等式f′(x)>0,f′(x)<0即可;
(2)对任意的a∈(1,2),当x0∈[1,2]时,都有f(x0)>m(1-a2),等价于f(x0)min>m(1-a2),用导数可求f(x0)min,构造函数g(a)=f(x0)min-m(1-a2)(1<a<2),问题转化为g(a)min>0(1<a<2),分类讨论可求出m的取值范围.
点评:本题考查综合运用导数求函数的单调区间、最值及函数恒成立问题,考查学生综合运用知识分析问题解决问题的能力,考查分类讨论思想的运用.
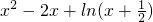 ,定义域为(-
,定义域为(- ,+∞).
,+∞).f′(x)=2x-2+
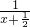 =2x-2+
=2x-2+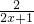 =
=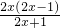 .
.由f′(x)>0,得
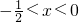 ,或x>
,或x> ;由f′(x)<0,得0<x<
;由f′(x)<0,得0<x< .
.所以函数f(x)的单调递增区间为(
 ,0),(
,0),( ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0, ).
).(2)y=f(x)的定义域为(-
 ,+∞).
,+∞).f′(x)=2x-a+
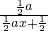 =2x-a+
=2x-a+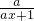 =
=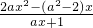 =
=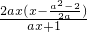 .
.当1<a<2时,
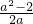 -1=
-1=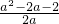 =
=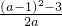 <0,即
<0,即 ,
,所以当1<x<2时,f′(x)>0,f(x)在[1,2]上单调递增,
所以f(x)在[1,2]上的最小值为f(1)=1-a+ln(
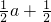 ).
).依题意,对任意的a∈(1,2),当x0∈[1,2]时,都有f(x0)>m(1-a2),
即可转化为对任意的a∈(1,2),1-a+ln(
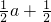 )-m(1-a2)>0恒成立.
)-m(1-a2)>0恒成立.设g(a)=1-a+ln(
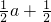 )-m(1-a2)(1<a<2).
)-m(1-a2)(1<a<2).则g′(a)=-1+
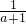 +2ma=
+2ma=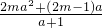 =
=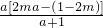 ,
,①当m≤0时,2ma-(1-2m)<0,且
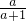 >0,所以g′(a)<0,
>0,所以g′(a)<0,所以g(a)在(1,2)上单调递减,且g(1)=0,则g(a)<0,与g(a)>0矛盾.
②当m>0时,g′(a)=
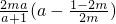 ,
,若
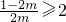 ,则g′(a)<0,g(a)在(1,2)上单调递减,且g(1)=0,g(a)<0,与g(a)>0矛盾;
,则g′(a)<0,g(a)在(1,2)上单调递减,且g(1)=0,g(a)<0,与g(a)>0矛盾;若1<
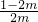 <2,则g(a)在(1,
<2,则g(a)在(1,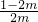 )上单调递减,在(
)上单调递减,在(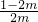 ,2)上单调递增,且g(1)=0,g(a)<g(1)=0,与g(a)>0矛盾;
,2)上单调递增,且g(1)=0,g(a)<g(1)=0,与g(a)>0矛盾;若
 ,则g(a)在(1,2)上单调递增,且g(1)=0,
,则g(a)在(1,2)上单调递增,且g(1)=0,则恒有g(a)>g(1)=0,所以
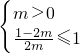 ,解得m
,解得m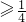 ,所以m的取值范围为[
,所以m的取值范围为[ ,+∞).
,+∞).分析:(1)当a=2时,求出f(x),在定义域内解不等式f′(x)>0,f′(x)<0即可;
(2)对任意的a∈(1,2),当x0∈[1,2]时,都有f(x0)>m(1-a2),等价于f(x0)min>m(1-a2),用导数可求f(x0)min,构造函数g(a)=f(x0)min-m(1-a2)(1<a<2),问题转化为g(a)min>0(1<a<2),分类讨论可求出m的取值范围.
点评:本题考查综合运用导数求函数的单调区间、最值及函数恒成立问题,考查学生综合运用知识分析问题解决问题的能力,考查分类讨论思想的运用.

练习册系列答案
相关题目
 .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a). .
. 时,f(x)的值域为[4,6],求a,b的值.
时,f(x)的值域为[4,6],求a,b的值. 函数
函数 .
.