题目内容
4.已知实数a,b满足$\frac{9}{{a}^{2}}$+$\frac{4}{{b}^{2}}$=1,则a2+b2的最小值是25.分析 利用基本不等式的性质即可得出.
解答 解:a2+b2=(a2+b2)($\frac{9}{{a}^{2}}$+$\frac{4}{{b}^{2}}$)=9+4+$\frac{9{b}^{2}}{{a}^{2}}$+$\frac{4{a}^{2}}{{b}^{2}}$≥13+2$\sqrt{\frac{9{b}^{2}}{{a}^{2}}•\frac{4{a}^{2}}{{b}^{2}}}$=13+12=25,当且仅当a2=15,b2=10取等号,
故a2+b2的最小值是25,
故答案为:25
点评 熟练掌握基本不等式的性质是解题的关键.

练习册系列答案
相关题目
14.下列函数是奇函数的是( )
| A. | f(x)=-|sin x| | B. | f(x)=cos(-|x|) | C. | f(x)=sin|x| | D. | f(x)=x•sin|x| |
15.复数z=i(1-$\frac{1}{i}$)在复平面上对应的点Z位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.三个数60.7,(0.7)6,log0.76的大小顺序是( )
| A. | (0.7)6<log0.76<60.7 | B. | (0.7)6<60.7<log0.76 | ||
| C. | log0.76<60.7<(0.7)6 | D. | log0.76<(0.7)6<60.7 |
16.已知函数y=|x-3|+1在区间[0,9]上的值域是( )
| A. | [4,7] | B. | [0,7] | C. | [1,7] | D. | [2,7] |
13.在锐角△ABC中,已知|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=1,S△ABC=$\sqrt{3}$,则$|{\overrightarrow{BC}}|$等于( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{17}$ | D. | 17 |
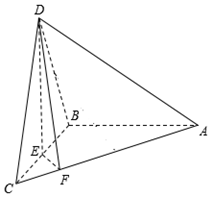 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,