题目内容
设椭圆的左焦点为F，AB为椭圆中过F的弦，试判断以AB为直径的圆与左准线的位置关系.
解：设M为弦AB的中点(即圆心)，A′，B′，M′分别是A，B，M的准线l上的射影，由椭圆第二定义，得|AB|=|AF|+|BF|=e(|AA′|+|BB′|).
∵0＜e＜1,
∴|AB|＜|AA′|+|BB′|=2|MM′|,
∴
＜|MM′|,
∴以AB为直径的圆与左准线相离.
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
（本小题满分12分）
设椭圆
的左焦点为F，O为坐标原点，已知椭圆中心关于直线
对称点恰好落在椭圆的左准线上。
（1）求过O、F并且与椭圆右准线l相切的圆的方程；
|
外的任意一点，过点P的直线PA、PB分别与椭圆相切于A、B两点。
，求直线
的方程。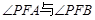
是否总是相等？若是，请给出证明。
的左焦点为F, 离心率为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为
. 
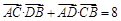, 求k的值.