题目内容
已知函数 ,其中
,其中 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(I)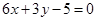 ;(II)详见解析.
;(II)详见解析.
解析试题分析:(I)求出导数即切线斜率,代入点斜式;(II)列表,依据参数分情况讨论,求最值.
试题解析:(Ⅰ)解: 的定义域为
的定义域为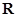 , 且
, 且 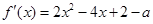 . 2分
. 2分
当 时,
时,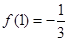 ,
,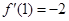 ,
,
所以曲线 在点
在点 处的切线方程为
处的切线方程为 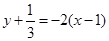 ,
,
即 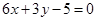 . 4分
. 4分
(Ⅱ)解:方程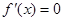 的判别式为
的判别式为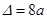 .
.
(ⅰ)当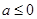 时,
时,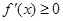 ,所以
,所以 在区间
在区间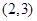 上单调递增,所以
上单调递增,所以 在区间
在区间
上的最小值是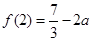 ;最大值是
;最大值是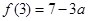 . 6分
. 6分
(ⅱ)当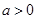 时,令
时,令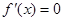 ,得
,得 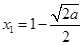 ,或
,或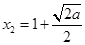 .
.  和
和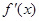 的情况如下:
的情况如下: 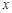
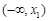
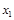
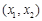
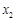
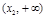
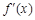
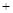

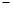

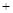
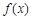
 练习册系列答案
练习册系列答案
寒假作业黄山书社系列答案
寒假作业安徽教育出版社系列答案
寒假作业深圳报业集团出版社系列答案
寒假作业内蒙古人民出版社系列答案
寒假作业人民教育出版社系列答案
寒假作业云南人民出版社系列答案
寒假作业宁夏人民教育出版社系列答案
寒假作业时代出版传媒股份有限公司系列答案
寒假作业华中科技大学出版社系列答案
复习计划100分寒假学期复习系列答案
相关题目
 (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时,
 上的最小值;
上的最小值; ,求证:
,求证: .
.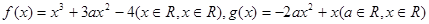 (Ⅰ)若函数
(Ⅰ)若函数 在
在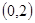 上单调递减,在区间
上单调递减,在区间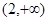 单调递增,求
单调递增,求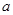 的值;
的值;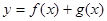 在
在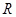 上有两个不同的极值点,求
上有两个不同的极值点,求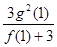 的取值范围;
的取值范围;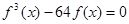 有且只有三个不同的实根,求
有且只有三个不同的实根,求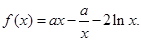
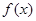 在
在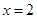 时有极值,求实数
时有极值,求实数 的值和
的值和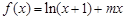
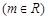 .
.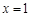 时,函数
时,函数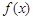 取得极大值,求实数
取得极大值,求实数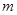 的值;
的值;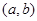 内存在导数,则存在
内存在导数,则存在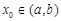 ,使得
,使得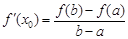 . 试用这个结论证明:若函数
. 试用这个结论证明:若函数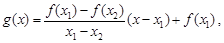 (其中
(其中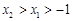 ),则对任意
),则对任意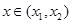 ,都有
,都有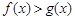 ;
;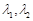 满足
满足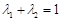 ,求证:对任意的实数
,求证:对任意的实数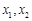 ,若
,若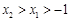 时,都
时,都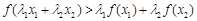 .
.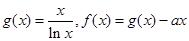
 的单调区间;
的单调区间; 在
在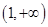 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;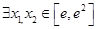 ,使
,使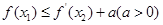 成立,求实数
成立,求实数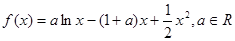
 的单调区间;
的单调区间;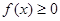 对定义域内的任意
对定义域内的任意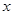 恒成立,求实数
恒成立,求实数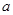 的取值范围.
的取值范围.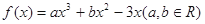 ,在点
,在点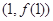 处的切线方程为
处的切线方程为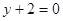 .
.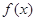 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值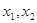 ,都有
,都有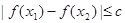 ,求实数
,求实数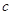 的最小值;
的最小值;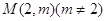 ,可作曲线
,可作曲线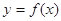 的三条切线,求实数
的三条切线,求实数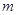 的取值范围.
的取值范围.