题目内容
已知函数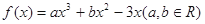 ,在点
,在点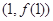 处的切线方程为
处的切线方程为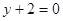 .
.
(Ⅰ)求函数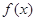 的解析式;
的解析式;
(Ⅱ)若对于区间 上任意两个自变量的值
上任意两个自变量的值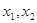 ,都有
,都有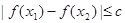 ,求实数
,求实数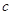 的最小值;
的最小值;
(Ⅲ)若过点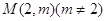 ,可作曲线
,可作曲线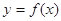 的三条切线,求实数
的三条切线,求实数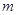 的取值范围.
的取值范围.
(1)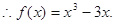
(2)4
(3)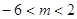
解析试题分析:(Ⅰ)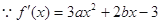
根据题意,得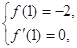 即
即
解得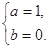
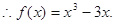
(Ⅱ)令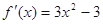
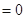 ,解得
,解得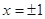
f(-1)=2, f(1)=-2,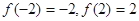
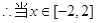 时,
时,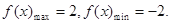
则对于区间[-2,2]上任意两个自变量的值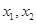 ,都有
,都有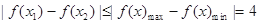
所以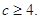 所以
所以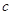 的最小值为4。
的最小值为4。
(Ⅲ)设切点为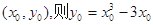
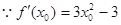 ,
, 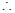 切线的斜率为
切线的斜率为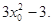
则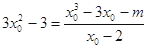
即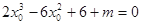 ,
,
因为过点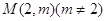 ,可作曲线
,可作曲线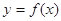 的三条切线
的三条切线
所以方程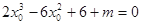 有三个不同的实数解
有三个不同的实数解
即函数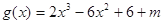 有三个不同的零点,
有三个不同的零点,
则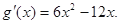
令
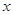
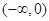
0 (0,2) 2 (2,+∞) 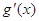
+ 0 — 0 + 

极大值 
 练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目
 ,其中
,其中 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. .若
.若 ,求
,求 的值;当
的值;当 时,求
时,求 的单调区间.
的单调区间.
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的极值.
的极值.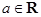 ,函数
,函数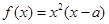 ,若
,若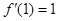 .
.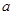 的值并求曲线
的值并求曲线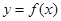 在点
在点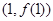 处的切线方程
处的切线方程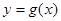 ;
;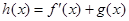 ,求
,求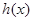 在
在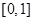 上的最大值与最小值.
上的最大值与最小值. .
. 图像上的点到直线
图像上的点到直线 距离的最小值为
距离的最小值为 ,求
,求 的值;
的值; 的不等式
的不等式 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数 定义域上的任意实数
定义域上的任意实数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数 ,试探究
,试探究

 及
及 ,
,
 两点连线的斜率为
两点连线的斜率为 ,问是否存在常数
,问是否存在常数 ,且
,且 ,当
,当 时有
时有 ,当
,当 时有
时有 ;若存在,求出
;若存在,求出 有极值,
有极值, 的取值范围;
的取值范围;