题目内容
已知函数
(
).
(1)当
时,求函数
的单调区间;
(2)当
时,取得极值，求函数在
上的最小值;
(1)单调增区间为
和
,单调减区间为
；
（2）
.
解析试题分析：(1)求导解
得
或
, 解
得
；
(2)当
时,取得极值, 所以
解得
，对求导，判断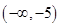在
,
递增,在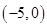
递减，分类讨论，求出最小值.
试题解析：(1)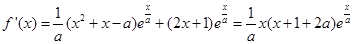
当时,
解得或, 解得 [来源:Z*xx*k.Com]
所以单调增区间为和,单调减区间为
(2)当时,取得极值, 所以
解得(经检验符合题意) 
↗
，（
）在
处取得最小值.
的值；
在
处的切线方程为
，求证：当
时，曲线
不可能在直线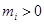
，（
）且
，试比较
与
的大小，并证明你的结论.
的图象如图，f(x)=6lnx+h(x).
)上是单调函数，求实数m的取值范围；
在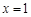
处取得极值.
的值；
的方程
在
上恰有两个不相等的实数根，求实数
的取值范围;
，使
成立，求实数
.
的单调性；
恒成立，证明：当
时，
.
(
).
时,判断
在定义域上的单调性；
上的最小值为
,求
的值；
在
上恒成立，试求
(
)．
的单调区间；
（
）的单调性证明：当
时，
；
,且
均为正实数, 
时，
．
，
.
，求函数
在区间
上的最值；
恒成立，求
的取值范围.
是自然对数的底数
，其中
．
，求曲线
在点
处的切线方程；
在区间
上的最大值和最小值．