题目内容
已知点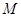 是椭圆
是椭圆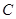 :
: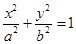
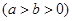 上一点,
上一点,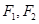 分别为
分别为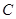 的左右焦点
的左右焦点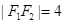 ,
,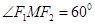 ,
,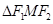 的面积为
的面积为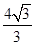 .
.
(Ⅰ)求椭圆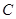 的方程;
的方程;
(Ⅱ)设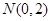 ,过点
,过点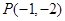 作直线
作直线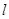 ,交椭圆
,交椭圆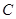 异于
异于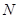 的
的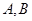 两点,直线
两点,直线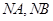 的斜率分别为
的斜率分别为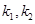 ,证明:
,证明: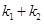 为定值.
为定值.
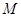 是椭圆
是椭圆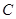 :
: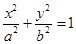
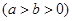 上一点,
上一点,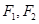 分别为
分别为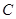 的左右焦点
的左右焦点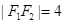 ,
,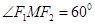 ,
,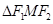 的面积为
的面积为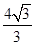 .
.(Ⅰ)求椭圆
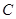 的方程;
的方程;(Ⅱ)设
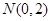 ,过点
,过点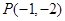 作直线
作直线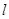 ,交椭圆
,交椭圆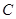 异于
异于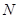 的
的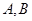 两点,直线
两点,直线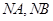 的斜率分别为
的斜率分别为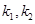 ,证明:
,证明: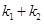 为定值.
为定值.(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:本题考查椭圆的定义、余弦定理及韦达定理的应用.第一问是利用三角形面积公式、余弦定理、椭圆的定义,三个方程联立,解出
 ,再根据
,再根据 的关系求
的关系求 ,本问分析已知条件是解题的关键;第二问是直线与椭圆相交于
,本问分析已知条件是解题的关键;第二问是直线与椭圆相交于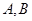 两点,先设出
两点,先设出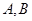 两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,但是在本问中需考虑直线的斜率是否存在,此题中蕴含了分类讨论的思想的应用.
两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,但是在本问中需考虑直线的斜率是否存在,此题中蕴含了分类讨论的思想的应用.试题解析:(Ⅰ)在
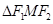 中,
中,由
 ,得
,得 .
.由余弦定理,得

 ,
,从而
 ,即
,即 ,从而
,从而 ,
,故椭圆
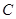 的方程为
的方程为 . 6分
. 6分(Ⅱ)当直线
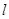 的斜率存在时,设其方程为
的斜率存在时,设其方程为 ,
,由
 ,得
,得 . 8分
. 8分设
 ,
, ,
, ,
, .
.从而
 . 11分
. 11分当直线
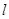 的斜率不存在时,得
的斜率不存在时,得 ,得
,得 .
.综上,恒有
 . 12分
. 12分
练习册系列答案
相关题目
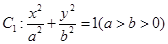 的离心率为
的离心率为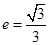 ,直线
,直线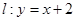 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆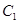 的短半轴长为半径的圆
的短半轴长为半径的圆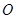 相切.
相切.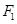 ,右焦点为
,右焦点为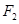 ,直线
,直线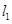 过点
过点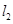 垂直于
垂直于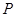 ,线段
,线段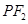 的垂直平分线交
的垂直平分线交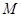 ,求点
,求点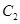 的方程;
的方程;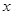 轴交于点
轴交于点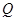 ,不同的两点
,不同的两点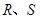 在
在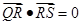 ,求
,求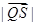 的取值范围.
的取值范围.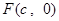 是椭圆
是椭圆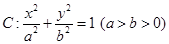 的右焦点,圆
的右焦点,圆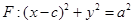 与
与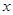 轴交于
轴交于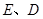 两点,
两点,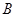 是椭圆
是椭圆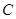 与圆
与圆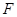 的一个交点,且
的一个交点,且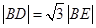
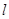 与
与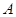 ,且
,且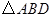 的面积为
的面积为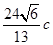 ,求椭圆
,求椭圆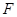 为抛物线
为抛物线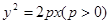 的焦点,抛物线上点
的焦点,抛物线上点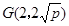 满足
满足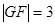

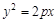 的方程;
的方程;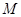 点的坐标为(
点的坐标为(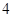 ,
, ),过点F作斜率为
),过点F作斜率为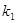 的直线与抛物线交于
的直线与抛物线交于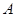 、
、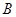 两点,
两点,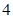 ,连结
,连结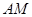 、
、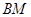 并延长交抛物线于
并延长交抛物线于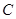 、
、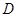 两点,设直线
两点,设直线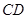 的斜率为
的斜率为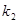 ,问
,问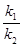 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.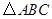 中,
中,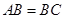 ,
, .若以
.若以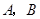 为焦点的椭圆经过点
为焦点的椭圆经过点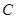 ,则该椭圆的离心率
,则该椭圆的离心率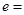 ( )
( )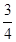

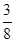
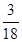
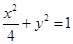 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于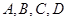 四点,则四边形
四点,则四边形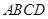 面积的最大值与最小值之差为( )
面积的最大值与最小值之差为( )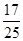
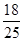
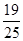
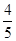
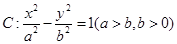 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线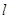 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若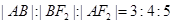 ,则双曲线的离心率是( )
,则双曲线的离心率是( )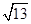
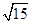
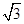
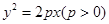 的焦点
的焦点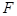 恰为双曲线
恰为双曲线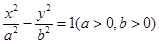 的右焦点,且两曲线交点的连线过点
的右焦点,且两曲线交点的连线过点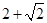
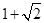
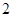
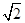
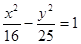 的左焦点为
的左焦点为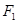 ,点
,点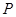 为双曲线右支上一点,且
为双曲线右支上一点,且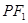 与圆
与圆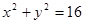 相切于点
相切于点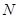 ,
,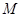 为线段
为线段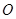 为坐标原点, 则
为坐标原点, 则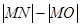 =
=