题目内容
将正偶数 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记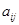 表示第
表示第 行和第
行和第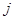 列的数,若
列的数,若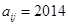 ,则
,则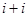 的值为( )
的值为( )
| | 第 列 列 | 第 列 列 | 第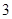 列 列 | 第 列 列 | 第 列 列 |
第 行 行 | |  |  |  |  |
第 行 行 |  | 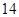 |  |  | |
第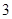 行 行 | | 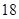 | 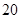 | 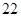 | 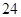 |
第 行 行 | 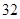 |  | 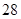 | 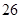 | |
第 行 行 | |  | 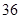 | 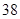 | 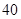 |
 |  |  |  |  |  |
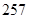 B.
B.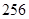 C.
C.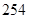 D.
D.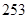
C
解析试题分析:由表所反映的信息来看,第 行的最大偶数为
行的最大偶数为 ,则
,则 ,由于
,由于 ,解得
,解得 ;另一方面奇数行的最大数位于第
;另一方面奇数行的最大数位于第 列,偶数行最大数位于第
列,偶数行最大数位于第 列,第
列,第 行最大数为
行最大数为 ,此数位于第
,此数位于第 行第
行第 列,因此
列,因此 位于第
位于第 行第
行第 列,所以
列,所以 ,
, ,故
,故 ,选C.
,选C.
考点:推理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据偶函数定义可推得“函数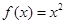 在
在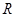 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
用反证法证明命题:“若a,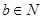 ,
,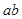 能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一个能被5整除 | D.a,b有一个不能被5整除 |
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
① ,这与三角形内角和为
,这与三角形内角和为 相矛盾,
相矛盾,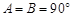 不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角
不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角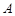 、
、 、
、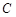 中有两个直角,不妨设
中有两个直角,不妨设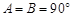 ;正确顺序的序号为 ( )
;正确顺序的序号为 ( )
| A.①②③ | B.③①② | C.①③② | D.②③① |
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )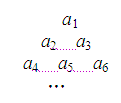
| A.247 | B.735 |
| C.733 | D.731 |
观察下列等式,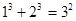 ,
,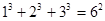 ,
,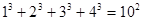 根据上述规律,
根据上述规律,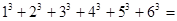 ( )
( )
A.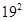 | B.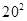 | C.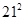 | D.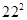 |
右图1是一个水平摆放的小正方体木块,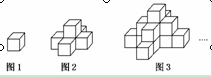
图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是( )
| A.25 | B.66 | C.91 | D.120 |
若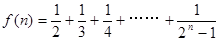 ,则
,则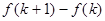 等于( )
等于( )
A.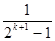 | B.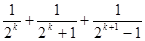 |
C.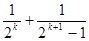 | D.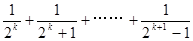 |
下列几种推理过程是演绎推理的是( )
| A.某校高三1班55人,2班54人,3班52人,由此得高三所有班级的人数超过50人 |
| B.由圆的周长C=πd推测球的表面积S=πd2 |
| C.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
D.在数列{an}中,a1=1,an=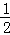 (an﹣1+ (an﹣1+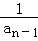 )(n≥2),由此归纳数列{an}的通项公式 )(n≥2),由此归纳数列{an}的通项公式 |