题目内容
已知a=(2,-1,-2),b=(0,-1,4),求a+b,a-b,3a+2b,a·b.
分析:空间向量的加、减、数乘运算与平面向量的加、减、数乘运算方法类似,向量的数量积等于它们对应坐标乘积的和.
解:因为a=(2,-1,-2),b=(0,-1,4),
所以a+b=(2,-1,-2)+(0,-1,4)=(2+0,-1+(-1),-2+4)=(2,-2,2).
a-b=(2,-1,-2)-(0,-1,4)=(2-0,-1-(-1),-2-4)=(2,0,-6).
3a+2b=3(2,-1,-2)+2(0,-1,4)=(3×2,3×(-1),3×(-2))+(2×0,2×(-1),2×4)=(6,-3,-6)+(0,-2,8)=(6,-5,2).
a·b=(2,-1,-2)·(0,-1,4)=2×0+(-1)×(-1)+(-2)×4=0+1-8=-7.
点拨:空间向量的加,减,数乘,数量积运算是今后利用向量知识解决立体几何知识的基础,必须熟练掌握,并且能够灵活地应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
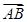 +
+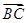 =
=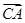 ;
;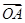 +
+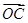 =
=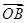 ;
;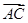 =
=