题目内容
已知函数f(x)=ax+xlnx(a∈R)
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈z时,不等式k(x-1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈z时,不等式k(x-1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的概念及应用
分析:(1)易求f′(x)=a+1+lnx,依题意知,当x≥e时,a+1+lnx≥0恒成立,即x≥e时,a≥(-1-lnx)max,从而可得a的取值范围;
(2)依题意,k<
对任意x>1恒成立,令g(x)=
则g′(x)=
,再令h(x)=x-lnx-2(x>1),易知h(x)在(1,+∞)上单增,从而可求得
g(x)min=x0∈(3,4),而k∈z,从而可得k的最大值.
(2)依题意,k<
| x+xlnx |
| x-1 |
| x+xlnx |
| x-1 |
| x-lnx-2 |
| (x-1)2 |
g(x)min=x0∈(3,4),而k∈z,从而可得k的最大值.
解答:
解:(1)∵f(x)=ax+xlnx,
∴f′(x)=a+1+lnx,又函数f(x)在区间[e,+∞)上为增函数,
∴当x≥e时,a+1+lnx≥0恒成立,
∴a≥(-1-lnx)max=-1-lne=-2,即a的取值范围为[-2,+∞);
(2)当x>1时,x-1>0,故不等式k(x-1)<f(x)?k<
,
即k<
对任意x>1恒成立.
令g(x)=
则g′(x)=
,
令h(x)=x-lnx-2(x>1),
则h′(x)=1-
=
>0⇒h(x)在(1,+∞)上单增.
∵h(3)=1-ln3<0,h(4)=2-ln4>0,
∴存在x0∈(3,4)使h(x0)=0,
即当1<x<x0时,h(x)<0,即g′(x)<0,
当x>x0时,h(x)>0,即g′(x)>0,∴g(x)在(1,x0)上单减,在(x0,+∞)上单增.
令h(x0)=x0-lnx0-2=0,即lnx0=x0-2,g(x)min=g(x0)=
=
=x0∈(3,4),
∴k<g(x)min=x0且k∈Z,
即kmax=3.
∴f′(x)=a+1+lnx,又函数f(x)在区间[e,+∞)上为增函数,
∴当x≥e时,a+1+lnx≥0恒成立,
∴a≥(-1-lnx)max=-1-lne=-2,即a的取值范围为[-2,+∞);
(2)当x>1时,x-1>0,故不等式k(x-1)<f(x)?k<
| f(x) |
| x-1 |
即k<
| x+xlnx |
| x-1 |
令g(x)=
| x+xlnx |
| x-1 |
| x-lnx-2 |
| (x-1)2 |
令h(x)=x-lnx-2(x>1),
则h′(x)=1-
| 1 |
| x |
| x-1 |
| x |
∵h(3)=1-ln3<0,h(4)=2-ln4>0,
∴存在x0∈(3,4)使h(x0)=0,
即当1<x<x0时,h(x)<0,即g′(x)<0,
当x>x0时,h(x)>0,即g′(x)>0,∴g(x)在(1,x0)上单减,在(x0,+∞)上单增.
令h(x0)=x0-lnx0-2=0,即lnx0=x0-2,g(x)min=g(x0)=
| x0(1+lnx0) |
| x0-1 |
| x0(1+x0-2) |
| x0-1 |
∴k<g(x)min=x0且k∈Z,
即kmax=3.
点评:本题考查利用导数研究函数的单调性及利用导数求闭区间上函数的最值,着重考查等价转化思想与函数恒成立问题,属于难题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
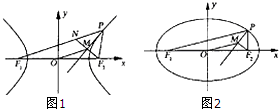 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、(0,a) |
| B、(0,b) |
| C、(b,a) |
| D、(0,c) |
已知双曲线
-
=1(a>0,b>0)的离心率为
,右焦点为F2(2
,0),点A1,A2分别为左、右顶点,点P为此双曲线在第一象限内的点,设tan∠PA1A2+tan∠PA2F2=m,则有( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| A、m<2 | B、m≤2 |
| C、m>2 | D、m≥2 |
在区间[0,1]内任取两个实数,则这两个实数的和大于
的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|