题目内容
7.已知函数f(x)=x2-πx,α,β,γ∈(0,π),且sinα=$\frac{1}{3}$,tanβ=$\frac{5}{4}$,cosγ=-$\frac{1}{3}$,则( )| A. | f(α)>f(β)>f(γ) | B. | f(α)>f(γ)>f(β) | C. | f(β)>f(α)>f(γ) | D. | f(β)>f(γ)>f(α) |
分析 根据函数f(x)是二次函数,开口向上,对称轴是x=$\frac{π}{2}$;再由题意求出α,β,γ的范围,即可得出f(α)、f(β)与f(γ)的大小关系.
解答 解:∵函数f(x)=x2-πx是二次函数,开口向上,且对称轴是x=$\frac{π}{2}$;
∴f(x)在(0,$\frac{π}{2}$)上单调递减,在($\frac{π}{2}$,π)单调递增;
又α,β,γ∈(0,π),且sinα=$\frac{1}{3}$<$\frac{1}{2}$,tanβ=$\frac{5}{4}$>1,cosγ=-$\frac{1}{3}$>-$\frac{1}{2}$,
∴α<$\frac{π}{6}$或α>$\frac{5π}{6}$,$\frac{π}{4}$<β<$\frac{π}{3}$,$\frac{π}{2}$<γ<$\frac{2π}{3}$,
∴f(α)>f(β)>f(γ).
故选:A.
点评 本题考查了二次函数与三角函数的单调性问题,是基础题目.

练习册系列答案
相关题目
15.设全集U={1,2,3,4,5,6,7},B={2,4,6},则∁UB=( )
| A. | {2,4,6} | B. | {1,3,5} | C. | {1,3,5,7} | D. | {1,3} |
16.复数z满足(3-2i)z=4+3i(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知$tanα=-\frac{3}{4}$,则sinα(sinα-cosα)=( )
| A. | $\frac{21}{25}$ | B. | $\frac{25}{21}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
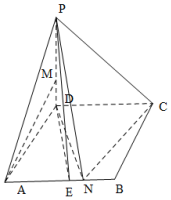 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,