题目内容
(本小题满分12分)已知椭圆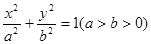 的左右焦点分别为
的左右焦点分别为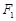 、
、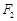 ,短轴两个端点为
,短轴两个端点为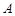 、
、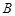 ,且四边形
,且四边形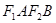 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若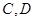 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点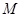 满足
满足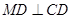 ,连接
,连接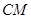 ,交椭圆于点
,交椭圆于点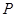 ;证明:
;证明: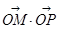 为定值;
为定值;
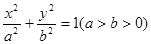 的左右焦点分别为
的左右焦点分别为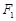 、
、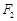 ,短轴两个端点为
,短轴两个端点为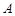 、
、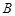 ,且四边形
,且四边形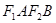 是边长为2的正方形。
是边长为2的正方形。(1)求椭圆方程;
(2)若
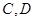 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点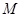 满足
满足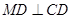 ,连接
,连接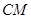 ,交椭圆于点
,交椭圆于点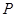 ;证明:
;证明: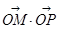 为定值;
为定值; 解:(1)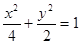 ;(2)见解析。
;(2)见解析。
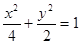 ;(2)见解析。
;(2)见解析。本试题主要是考查了椭圆的方程以及直线与椭圆的 位置关系的运用。
(1)利用已知条件得到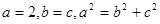 ,
,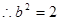 ,,进而得到椭圆方程。
,,进而得到椭圆方程。
(2)因为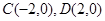 ,设
,设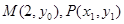 ,则
,则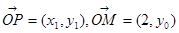 。
。
直线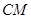 :
: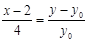 ,即
,即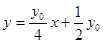 ,那么联立方程则利用韦达定理和向量的数量积公式得到结论。
,那么联立方程则利用韦达定理和向量的数量积公式得到结论。
解:(1)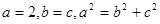 ,
,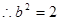 ,
, 椭圆方程为
椭圆方程为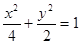 。4分
。4分
(2)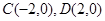 ,设
,设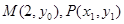 ,则
,则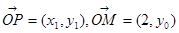 。
。
直线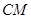 :
: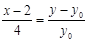 ,即
,即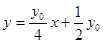 ,……………………………6分
,……………………………6分
代入椭圆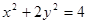 得
得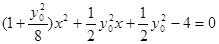 。…………8分
。…………8分
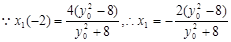 ,
,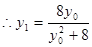 。
。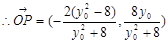 ,…10分
,…10分
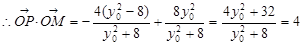 (定值)。…………12分
(定值)。…………12分
(1)利用已知条件得到
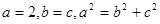 ,
,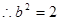 ,,进而得到椭圆方程。
,,进而得到椭圆方程。(2)因为
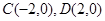 ,设
,设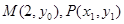 ,则
,则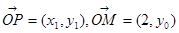 。
。直线
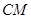 :
: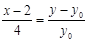 ,即
,即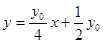 ,那么联立方程则利用韦达定理和向量的数量积公式得到结论。
,那么联立方程则利用韦达定理和向量的数量积公式得到结论。解:(1)
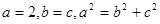 ,
,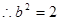 ,
, 椭圆方程为
椭圆方程为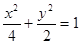 。4分
。4分(2)
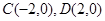 ,设
,设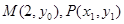 ,则
,则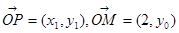 。
。直线
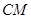 :
: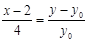 ,即
,即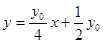 ,……………………………6分
,……………………………6分代入椭圆
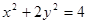 得
得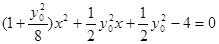 。…………8分
。…………8分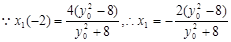 ,
,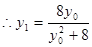 。
。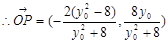 ,…10分
,…10分
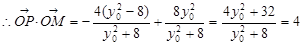 (定值)。…………12分
(定值)。…………12分
练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
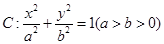 ,
,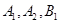 是椭圆
是椭圆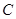 的顶点,若椭圆
的顶点,若椭圆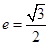 ,且过点
,且过点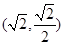 .
.
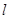 ,使得
,使得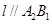 ,且与椭圆
,且与椭圆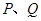 两点(异于椭圆
两点(异于椭圆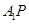 和直线
和直线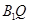 的倾斜角分别是
的倾斜角分别是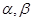 ,求证:
,求证: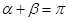 .
.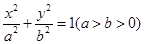 的左顶点为
的左顶点为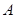 ,上顶点为
,上顶点为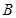 ,右焦点为
,右焦点为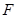 .设线段
.设线段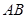 的中点为
的中点为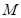 ,若
,若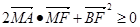 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .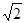 ,焦点到相应准线的
,焦点到相应准线的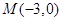 ,点
,点 ,动点
,动点 满足
满足 ,则点
,则点


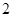
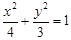 的左、右焦点分别为
的左、右焦点分别为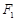 、
、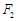 ,直线
,直线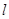 经过点
经过点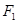 与椭圆交于
与椭圆交于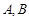 两点。
两点。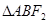 的周长;
的周长;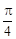 ,求
,求
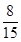
 上一点M到直线x+2y-10=0的距离的最小值为( )
上一点M到直线x+2y-10=0的距离的最小值为( )