Question

【题目】已知△ABC中， =λ （0＜λ＜1），cosC= ，cos∠ADC= ．
（1）若AC=5．BC=7，求AB的大小；
（2）若AC=7，BD=10，求△ABC的面积．

Answer 1

【答案】
（1）解：∵ ，∴D在边BC上，且不与B，C重合，如图所示，

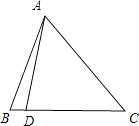
若AC=5，BC=7，∵ ；

∴在△ABC中由余弦定理得：

AB2=AC2+BC2﹣2ACBCcosC

=

=32；

∴ ；

（2）解：cosC= ， ；

∴ ；

∴sin∠DAC=sin[π﹣（C+∠ADC）]

=sin（C+∠ADC）

=sinCcos∠ADC+cosCsin∠ADC

=

= ；

又AC=7；

∴在△ACD中由正弦定理得： ；

即 ；

∴DC=5；

∴BC=BD+DC=15；

∴

【解析】（1）在△ABC中， ，这样根据余弦定理即可求出AB2的值，从而求出AB的大小；（2）可由cosC和cos∠ADC的值求出sinC和sin∠ADC的值，从而由sin∠DAC=sin（C+∠ADC）及两角和的正弦公式即可求出sin∠DAC的值，这样在△ACD中，由正弦定理即可求出DC的大小，从而得出BC的大小，这样由三角形的面积公式即可求出△ABC的面积．