题目内容
【题目】已知f(x)＝(ex－a)2＋(e－x－a)2(a≥0)．
(1)将f(x)表示成u(其中u＝
)的函数；
(2)求f(x)的最小值．
【答案】（1）g(u)＝4u2－4au＋2a2－2(u≥1)（2）f(x)min＝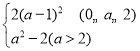
【解析】
（1）
展开后整理成关于
的形式，换元即可（2）由（1）知换元后函数为关于
的二次函数，根据对称轴分类讨论即可求解.
(1)将f(x)展开重新配方得，f(x)＝(ex＋e－x)2－2a(ex＋e－x)＋2a2－2.
令u＝
，则
，得g(u)＝4u2－4au＋2a2－2(u≥1)．
(2)∵g(u)的对称轴是u＝
，a≥0，
∴当0≤a≤2时，则当u＝1时，g(u)有最小值，此时g(u)min＝g(1)＝2(a－1)2.
当a＞2时，则当u＝时，g(u)有最小值，此时g(u)min＝g
＝a2－2.
∴f(x)的最小值为f(x)min＝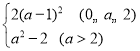
练习册系列答案
相关题目
