题目内容
求下列函数的单调区间:(1)y=sin(x-![]() );
);
(2)y=cos2x.
思路分析:本题主要考查复合函数的单调区间的求法.可依据y=sinx(x∈R)和y=cosx(x∈R)的单调区间及复合函数单调性原则求单调区间.
解:(1)令u=x-![]() ,函数y=sinu的递增、递减区间分别为[2kπ-
,函数y=sinu的递增、递减区间分别为[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z,[2kπ+
],k∈Z,[2kπ+![]() ,2kπ+
,2kπ+![]() ],k∈Z.
],k∈Z.
∴y=sin(x-![]() )的递增、递减区间分别由下面的不等式确定.
)的递增、递减区间分别由下面的不等式确定.
2kπ-![]() ≤x-
≤x-![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
2kπ+![]() ≤x-
≤x-![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
得2kπ-![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,k∈Z,
,k∈Z,
2kπ+![]() ≤x≤2kπ+116π,k∈Z.
≤x≤2kπ+116π,k∈Z.
∴函数y=sin(x-![]() )的递增区间、递减区间分别是
)的递增区间、递减区间分别是
[2kπ-![]() ,2kπ+
,2kπ+![]() ],k∈Z,
],k∈Z,
[2kπ+![]() ,2kπ+116π],k∈Z.
,2kπ+116π],k∈Z.
(2)函数y=cos2x的单调递增区间、单调递减区间分别由下面的不等式确定2kπ-π≤2x≤2kπ(k∈Z),2kπ≤2x≤2kπ+π,k∈Z.
∴kπ-![]() ≤x≤kπ,k∈Z,kπ≤x≤kπ+
≤x≤kπ,k∈Z,kπ≤x≤kπ+![]() ,k∈Z.
,k∈Z.
∴函数y=cos2x的单调递增区间、单调递减区间分别为
[kπ-![]() ,kπ],k∈Z,[kπ,kπ+
,kπ],k∈Z,[kπ,kπ+![]() ],k∈Z.
],k∈Z.

练习册系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;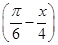 .
.