题目内容
已知Sn=1+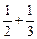 +…+
+…+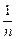 ,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-
,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-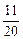 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.
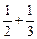 +…+
+…+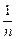 ,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-
,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-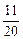 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.m> 且m≠2
且m≠2
 且m≠2
且m≠2∵Sn=1+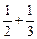 +…+
+…+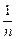 .(n∈N*)
.(n∈N*)

∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴f(n) min=f(2)=
∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2-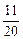 [log(m-1)m]2恒成立
[log(m-1)m]2恒成立
只要 >[logm(m-1)]2-
>[logm(m-1)]2-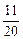 [log(m-1)m]2成立即可
[log(m-1)m]2成立即可
由 得m>1且m≠2
得m>1且m≠2
此时设[logm(m-1)]2=t 则t>0
于是 解得0<t<1
解得0<t<1
由此得0<[logm(m-1)]2<1
解得m> 且m≠2.
且m≠2.
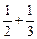 +…+
+…+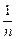 .(n∈N*)
.(n∈N*)
∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴f(n) min=f(2)=

∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2-
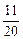 [log(m-1)m]2恒成立
[log(m-1)m]2恒成立只要
 >[logm(m-1)]2-
>[logm(m-1)]2-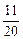 [log(m-1)m]2成立即可
[log(m-1)m]2成立即可由
 得m>1且m≠2
得m>1且m≠2此时设[logm(m-1)]2=t 则t>0
于是
 解得0<t<1
解得0<t<1由此得0<[logm(m-1)]2<1
解得m>
 且m≠2.
且m≠2.
练习册系列答案
相关题目
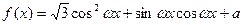 (其中
(其中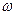 >0,
>0,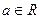 ),且
),且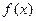 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为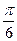 .(1)求
.(1)求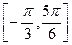 上的最小值为
上的最小值为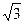 ,求a的值.
,求a的值.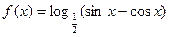 (1)求f(x)的定义域;(2)判断f(x)的奇偶性。
(1)求f(x)的定义域;(2)判断f(x)的奇偶性。 ,
, 的表达式是( )
的表达式是( )



 则
则 .
. 的定义域为______________________________。
的定义域为______________________________。 的最小正周期为( )
的最小正周期为( )



 =__________.
=__________.