题目内容
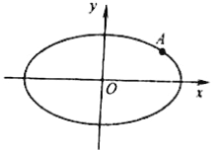
【题目】如图,在平面直角坐标系xOy中,椭圆E:![]() 的离心率为
的离心率为![]() ,点A(2,1)是椭圆E上的点.
,点A(2,1)是椭圆E上的点.
(1)求椭圆E的方程;
(2)过点A作两条互相垂直的直线l1,l2分別与椭圆E交于B,C两点,己知△ABC的面积为![]() ,求直线BC的方程.
,求直线BC的方程.
【答案】(1)![]() (2)x=
(2)x=![]() 或x-4y-2=0
或x-4y-2=0
【解析】
(1)将点![]() 的坐标代入椭圆方程,结合
的坐标代入椭圆方程,结合![]() ,解方程组求得
,解方程组求得![]() 的值,从而得到椭圆方程.(2)首先考虑直线
的值,从而得到椭圆方程.(2)首先考虑直线![]() 斜率不存在的情况,此时面积不合题意.当直线
斜率不存在的情况,此时面积不合题意.当直线![]() 斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出
斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出![]() ,同理求得
,同理求得![]() ,再用三角形面积为
,再用三角形面积为![]() 列方程,求得直线的斜率,由此求得
列方程,求得直线的斜率,由此求得![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 的方程.
的方程.
解:(1) 因为椭圆E的离心率为![]() ,所以
,所以![]() =
=![]() ,
,
又因为a2=b2+c2=2c2,所以a2=2b2=2c2,
因为点A(2,1)是椭圆E上的点,所以![]() +
+![]() =1
=1
解得b2=3,a2=6,
所以椭圆E的标准方程是![]() +
+![]() =1.
=1.
(2)当AB的斜率不存在或为0时,AB=4或2,此时△ABC的面积为4,不合题意舍去;
当AB的斜率存在且不为0时,设AB的斜率为k,则直线AB方程为y-1=k(x-2),
由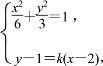 解得
解得![]() 或
或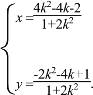
AB=![]() |
|![]() -2|=
-2|=![]() |
|![]() |,
|,
同理将上式中的k用-![]() 替换,得AC=
替换,得AC=![]() |
|![]() |,
|,
因为△ABC的面积为![]() ,所以
,所以![]() AB AC=
AB AC=![]()
![]() |
|![]() |
|![]() |
|![]() |=
|=![]() ,
,
化简得![]() =
=![]() ,
,
当k2≥1时,原方程可化为8k4-25k2-28=0,解得k2=4,
当k2≤1时,解得k2=![]() ,
,
即k=2或-2或![]() 或-
或-![]() ,
,
当AB的斜率2时,AC的斜率-![]() ,此时B点坐标(
,此时B点坐标(![]() ,-
,-![]() ),C点坐标(
),C点坐标(![]() ,
,![]() ),
),
此时直线BC的方程为x=![]() ,
,
当AB的斜率-2时,AC的斜率![]() ,此时B点坐标(
,此时B点坐标(![]() ,
,![]() ),C点坐标(-2,-1),
),C点坐标(-2,-1),
此时直线BC的方程为x-4y-2=0,
综上,直线BC的方程为x=![]() 或x-4y-2=0.
或x-4y-2=0.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

