题目内容
【题目】已知函数
的定义域是使得解析式有意义的x集合，如果对于定义域内的任意实数x，函数值均为正，则称此函数为“正函数”.
（1）证明函数
是“正函数”；
（2）如果函数
不是“正函数”，求正数a的取值范围.
（3）如果函数
是“正函数”，求正数a的取值范围.
【答案】（1）证明见解析，（2）
（3）
【解析】
（1）有题知：
，即证.
（2）首先讨论当
时，显然
不是“正函数”. 当
时，从反面入手，假设
是“正函数”，求出
的范围，再取其补集即可.
（3）根据题意得到：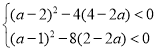
或
，解方程和不等式组即可.
（1）
.
函数值恒为正数，故函数
是“正函数”.
（2）当时，
，
显然不是“正函数”.
当时
假设为“正函数”.则恒大于零.
.
所以
，即
所以不是“正函数”时，
.
综上：
.
（3）有题知：若函数
是“正函数”，
则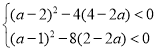或.
解得：
或
.
练习册系列答案
相关题目
