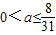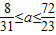题目内容

若方程2a•9sinx+4a•3sinx+a-8=0有解，则a的取值范围是（　　）
A．a＞0或a≤-8B．a＞0C．0＜a≤
8
31
D．
8
31
≤a≤
72
23
若方程2a•9sinx+4a•3sinx+a-8=0有解，则
等价于求a=
8
2•9sinx+4•3sinx+1
的值域
∵3sinx∈[
1
3
，3]
∴2•9sinx+4•3sinx+1∈[
23
9
，31]
则a的取值范围为
8
31
≤a≤
72
23

故选D．
练习册系列答案
相关题目
若方程2a•9sinx+4a•3sinx+a-8=0有解，则a的取值范围是（　　）
A、a＞0或a≤-8
B、a＞0
C、0＜a≤
8
31
D、
8
31
≤a≤
72
23
若方程2a•9sinx+4a•3sinx+a-8=0有解，则a的取值范围是
8
31
≤a≤
72
23
8
31
≤a≤
72
23
．
若方程2a•9sinx+4a•3sinx+a-8=0有解，则a的取值范围是（ ）
A．a＞0或a≤-8
B．a＞0
C．
D．
若方程2a•9sinx+4a•3sinx+a-8=0有解，则a的取值范围是（ ）
A．a＞0或a≤-8
B．a＞0
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网