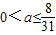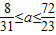Question

若方程2a•9^sinx+4a•3^sinx+a-8=0有解，则a的取值范围是

8

31

≤a≤

72

23

．

Answer 1

分析：令3^sinx=t，则由sinx∈[-1，1]，得t∈[

1

3

，3]，原方程化为关于t的一元二次方程，在区间[

1

3

，3]上有解．然后将方程变形为a=

8

2t 2+4t+1

，讨论右边的函数在区间[

1

3

，3]上的值域，可得出a的取值范围．

解答：解：令3^sinx=t，则由sinx∈[-1，1]，得t∈[

1

3

，3]
原方程变成：2at²+4at+a-8=0，在区间[

1

3

，3]上面有解
移项，解出a，得a=

8

2t 2+4t+1

因为2t²+4t+1=2（t+1）²-1，t∈[

1

3

，3]
所以2t²+4t+1∈[

23

9

，31]
因此，

8

2t 2+4t+1

∈[

8

31

，

72

23

]
故答案为：

8

31

≤a≤

72

23

点评：本题考查了指数型方程的解的知识点，属于中档题．变量分离，通过讨论函数的值域，是求解本题的关键．