题目内容
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:
(
>0),已知过点P(-2,-4)的直线l的参数方程为:
（t为参数）,直线l与曲线C分别交于M,N两点．
(1)写出曲线C和直线l的普通方程；
(2)若|PM|,|MN|,|PN|成等比数列,求的值．
(1) 曲线C: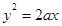
, 直线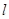
的普通方程为
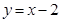；(2)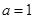 
．
解析试题分析：(1) 由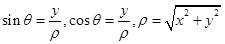
代入可得曲线C普通方程，直线l参数方程
，
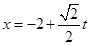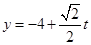两式相减消去参数
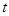，可得直线l的普通方程；(2)设两交点M,N对应的参数分别为t1,t2，将直线的参数方程代入抛物线方程可得
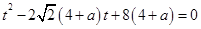，韦达定理求出
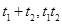，又|MN|2=|PM|·|PN|得(t1-t2)2=(t1+t2)2-4t1·t2=t1·t2,解得．
解：(1)由得曲线C: 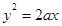,消去参数t可求得,
直线l的普通方程为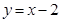． 4分
(2)直线l的参数方程为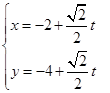
(t为参数),
代入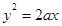,得,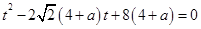
设两交点M,N对应的参数分别为t1,t2,
则有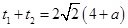
,
．
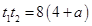因为|MN|2=|PM|·|PN|,所以(t1-t2)2=(t1+t2)2-4t1·t2=t1·t2,
解得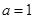． 12分
考点：极坐标方程与直角坐标方程的转化,参数方程．
练习册系列答案
相关题目
，圆M的参数方程为
。
中，已知点
，曲线
的参数方程为
为参数）.以原点为极点，
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
与直线
、
，求
的值.
ρ·cos
＋6＝0.
上一点，O为原点．若直线OP的倾斜角为
，求点
的直角坐标．
的极坐标方程是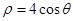
，以极点为原点，极轴为
轴正方向建立平面直角坐标系，直线l的参数方程是
(
为参数).
、
两点，点
的直角坐标为(2，1)，若
，求直线l的普通方程.
sin
，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的方程为y＝2x＋1，判断直线l和圆C的位置关系．
轴的正半轴重合，且两坐标系有相同的长度单位，圆C的参数方程为
（
为参数），点Q的极坐标为
。
过点Q且与圆C交于M，N两点，求当弦MN的长度为最小时，直线
且与极轴垂直的直线交曲线
于A、B两点，则
____ _