题目内容
对于函数f(x)=bx3+ax2-3x.
(1)若f(x)在x=1和x=3处取得极值,且f(x)的图象上每一点的切线的斜率均不超过2sintcost-2 cos2t+
cos2t+ ,试求实数t的取值范围;
,试求实数t的取值范围;
(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所围成的图形的面积S.
(1)若f(x)在x=1和x=3处取得极值,且f(x)的图象上每一点的切线的斜率均不超过2sintcost-2
 cos2t+
cos2t+ ,试求实数t的取值范围;
,试求实数t的取值范围;(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所围成的图形的面积S.
(1)k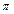 +
+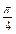 ≤t≤k
≤t≤k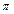 +
+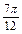 ,k∈Z(2)面积为S=
,k∈Z(2)面积为S=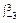 (1-
(1-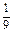 a2)da=4
a2)da=4
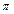 +
+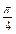 ≤t≤k
≤t≤k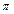 +
+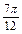 ,k∈Z(2)面积为S=
,k∈Z(2)面积为S=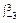 (1-
(1-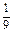 a2)da=4
a2)da=4 (1)由f(x)=bx3+ax2-3x,
则f′(x)=3bx2+2ax-3,
∵f(x)在x=1和x=3处取得极值,
∴x=1和x=3是f′(x)=0的两个根且b≠0.
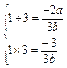
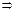
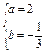 .
.
∴f′(x)=-x2+4x-3.
∵f(x)的图象上每一点的切线的斜率不超过
2sintcost-2 cos2t+
cos2t+ ,
,
∴f′(x)≤2sintcost-2 cos2t+
cos2t+ 对x∈R恒成立,
对x∈R恒成立,
而f′(x)=-(x-2)2+1,其最大值为1.
故2sintcost-2 cos2t+
cos2t+ ≥1
≥1
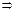 2sin(2t-
2sin(2t-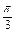 )≥1
)≥1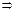 2k
2k +
+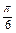 ≤2t-
≤2t-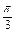 ≤2k
≤2k +
+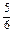
 ,k∈Z
,k∈Z
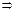 k
k +
+ ≤t≤k
≤t≤k +
+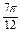 ,k∈Z.
,k∈Z.
(2)当b=0时,由f(x)在R上单调,知a=0.
当b≠0时,由f(x)在R上单调
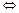 f′(x)≥0恒成立,或者f′(x)≤0恒成立.
f′(x)≥0恒成立,或者f′(x)≤0恒成立.
∵f′(x)=3bx2+2ax-3,
∴Δ=4a2+36b≤0可得b≤-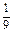 a2.
a2.
从而知满足条件的点P(a,b)在直角坐标平面aOb上形成的轨迹所围成的图形是由曲线b=-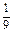 a2与直线b=-1所围成的封闭图形,
a2与直线b=-1所围成的封闭图形,
其面积为S=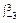 (1-
(1-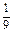 a2)da=4.
a2)da=4.
则f′(x)=3bx2+2ax-3,
∵f(x)在x=1和x=3处取得极值,
∴x=1和x=3是f′(x)=0的两个根且b≠0.
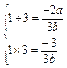
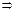
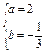 .
.∴f′(x)=-x2+4x-3.
∵f(x)的图象上每一点的切线的斜率不超过
2sintcost-2
 cos2t+
cos2t+ ,
,∴f′(x)≤2sintcost-2
 cos2t+
cos2t+ 对x∈R恒成立,
对x∈R恒成立,而f′(x)=-(x-2)2+1,其最大值为1.
故2sintcost-2
 cos2t+
cos2t+ ≥1
≥1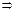 2sin(2t-
2sin(2t-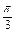 )≥1
)≥1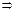 2k
2k +
+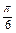 ≤2t-
≤2t-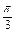 ≤2k
≤2k +
+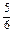
 ,k∈Z
,k∈Z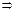 k
k +
+ ≤t≤k
≤t≤k +
+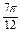 ,k∈Z.
,k∈Z.(2)当b=0时,由f(x)在R上单调,知a=0.
当b≠0时,由f(x)在R上单调
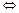 f′(x)≥0恒成立,或者f′(x)≤0恒成立.
f′(x)≥0恒成立,或者f′(x)≤0恒成立.∵f′(x)=3bx2+2ax-3,
∴Δ=4a2+36b≤0可得b≤-
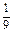 a2.
a2.从而知满足条件的点P(a,b)在直角坐标平面aOb上形成的轨迹所围成的图形是由曲线b=-
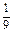 a2与直线b=-1所围成的封闭图形,
a2与直线b=-1所围成的封闭图形,其面积为S=
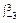 (1-
(1-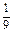 a2)da=4.
a2)da=4.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
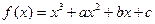 图像上一点
图像上一点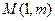 处的切线方程为
处的切线方程为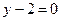 ,其中
,其中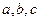 为常数.
为常数. 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用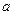 表示);
表示);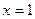 不是函数
不是函数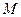 对称.
对称.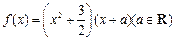 .
.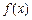 的图象上有与
的图象上有与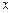 轴平行的切线,求
轴平行的切线,求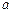 的范围;
的范围;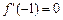 ,(Ⅰ)求函数
,(Ⅰ)求函数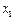 ,
,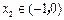 ,不等式
,不等式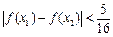 恒成立.
恒成立.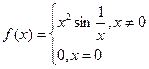 的导数
的导数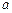 为实数,
为实数,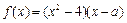 ,
,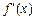 ;
;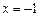 是函数
是函数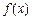 的极值点,求
的极值点,求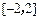 上的最大值和最小值;
上的最大值和最小值;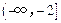 和
和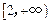 上都是递增的,求
上都是递增的,求 ;
; );
); .
.
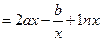
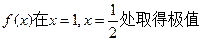 ,
, 

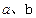 的值;
的值;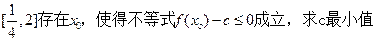
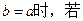
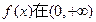 上是单调函数,求
上是单调函数,求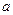 的取值范围。
的取值范围。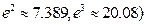
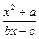 (b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–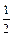 .(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (
.(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (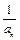 ) = 1,其中Sn为{an}的前n项和.求证:
) = 1,其中Sn为{an}的前n项和.求证: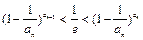 .
. ,若满足
,若满足 ,则必有( )
,则必有( ) B
B 
 D
D 